
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 是
是![]() 内部一点,
内部一点,![]() ,点
,点![]() 是边
是边![]() 上一点,若
上一点,若![]() 平分
平分![]() ,
,![]() ,则
,则![]() ______°
______°
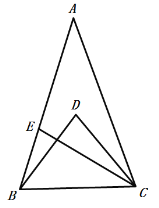
【答案】80
【解析】
根据角平分线得到∠ACE=2∠ACD,再根据角的和差关系得到∠ECB =∠ACB-2∠ACD,然后利用外角定理得到∠ABC+∠ECB=100°,代换化简得出∠ACB-∠ACD=50°,即∠DCB=50°,从而求出∠BDC即可.
∵CD平分∠ACE,
∴∠ACE=2∠ACD=2∠ECD,
∴∠ECB=∠ACB-∠ACE=∠ACB-2∠ACD,
∵∠AEC=100°,
∴∠ABC+∠ECB=100°,
∴∠ABC+∠ACB-2∠ACD=100°,
∵AB=AC,
∴∠ABC=∠ACB,
∴2∠ACB-2∠ACD=100°,
∴∠ACB-∠ACD=50°,即∠DCB=50°,
∵DB=DC,
∴∠DBC=∠DCB,
∴∠BDC=180°-2∠DCB=180°-2×50°=80°.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】(1).如图①,已知AB∥CD,求证:∠A+∠C=∠E
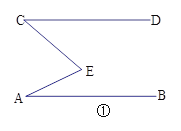
(2)直接写出当点E的位置分别如图②、图③、图④的情形时∠A、∠C、∠AEC之间的关系.
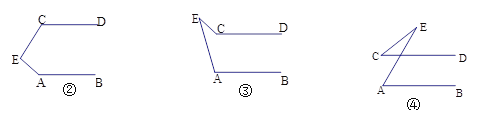
②中∠C、∠A、∠AEC之间的关系为 ;
③中∠C、∠A、∠AEC之间的关系为 ;
④中∠C、∠A、∠AEC之间的关系为 ;
(3)在(2)中的3中情形中任选一种进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图所示,给出下列说法:
的图象如图所示,给出下列说法:
①![]() ;②方程
;②方程![]() 的根为
的根为![]() ,
,![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() 随
随![]() 值的增大而增大;⑤当
值的增大而增大;⑤当![]() 时,
时,![]() .
.
其中正确的个数是

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择,李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家,设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:
地铁站 | A | B | C | D | E |
x(千米) | 8 | 9 | 10 | 11.5 | 13 |
y1(分钟) | 18 | 20 | 22 | 25 | 28 |
(1)求y1关于x的函数解析式;
(2)李华骑单车的时间(单位:分钟)也受x的影响,其关系可以用y2=![]() x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=![]() ,BC=8.
,BC=8.
(1)动手操作:
利用尺规作以AC为直径的圆O,并标圆O与AB的交点D,与BC的交点E,连接DE、CE(保留作图痕迹,不写作法)
(2)综合应用:
在你所作的图中,①求证:DE=CE;②求DC的长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线![]() 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:

(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周的某一天,小王全家上午8时自驾小汽车从家里出发,到“番茄农庄”游玩,小汽车离家的距离![]() (千米)与小汽车离家后时间
(千米)与小汽车离家后时间![]() (时)的关系可以用图中的折线表示,根据图像提供的有关信息,解答下列问题:
(时)的关系可以用图中的折线表示,根据图像提供的有关信息,解答下列问题:

(1)“番茄农庄”离家________千米;
(2)小王全家在“番茄农庄”游玩了________小时;
(3)去时小汽车的平均速度是________千米/小时;
(4)回家时小汽车的平均速度是________千米/小时.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com