
 数学课上,王老师在黑板上出示了一道问题让大家回答:题目如下
数学课上,王老师在黑板上出示了一道问题让大家回答:题目如下分析 (1)当点C在线段AB的延长线上时,AB=5,如果点O是线段AB的中点,则线段OB=$\frac{1}{2}$AB,再根据线段的和差,可得答案.
(2)当点C在线段AB上时,AB=5,如果点O是线段AB的中点,则线段OB=$\frac{1}{2}$AB,再根据线段的和差,可得答案.
解答 解:(1)因为 AB=5cm
又因为 O是线段AB的中点,
所以OA=OB=$\frac{1}{2}$AB
所以OA=OB=2.5.
因为OC=OB+BC
又因为BC=3cm.
所以OC=5.5,
故答案为:$\frac{1}{2}$AB,OB,BC,5.5;
(2)AB=5cm
又因为 O是线段AB的中点,
所以OA=OB=$\frac{1}{2}$AB
所以OA=OB=2.5.
因为OC=BC-OB,
又因为BC=3cm.
OC=3-2.5=0.5cm.
点评 本题考查了两点间的距离,利用线段中点的性质得出OB的长是解题关键,又利用了线段的和差.


 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:选择题
| A. | sinA=$\frac{\sqrt{2}}{2}$,sinB=$\frac{\sqrt{2}}{2}$ | B. | cosA=$\frac{1}{2}$,cosB=$\frac{\sqrt{3}}{2}$ | C. | sinA=$\frac{\sqrt{2}}{2}$,tanB=$\sqrt{3}$ | D. | sinA=$\frac{\sqrt{3}}{2}$,cosB=$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
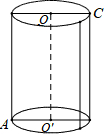 如图,有一个圆柱,它的高等于8cm,底面半径等于5cm,在圆柱的下底面点A处有一只蚂蚁,它想吃到上底面与点A相对的点C处的食物,需要爬行的最短路是多少?(π的值取3)
如图,有一个圆柱,它的高等于8cm,底面半径等于5cm,在圆柱的下底面点A处有一只蚂蚁,它想吃到上底面与点A相对的点C处的食物,需要爬行的最短路是多少?(π的值取3)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>2 | B. | m>-3 | C. | m≥-3 | D. | -3<m<2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
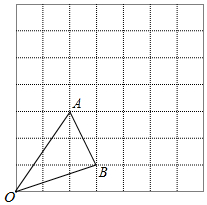 如图,在7×7的正方形网格中有一△OAB,其中点O、A、B均在图中格点上,观察图形并按要求回答问题:
如图,在7×7的正方形网格中有一△OAB,其中点O、A、B均在图中格点上,观察图形并按要求回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com