
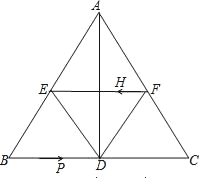
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,E点F点分别为AB,AC的中点.
(1)求证:四边形AEDF是菱形;
(2)求菱形AEDF的面积;
(3)若H从F点出发,在线段FE上以每秒2cm的速度向E点运动,点P从B点出发,在线段BC上以每秒3cm的速度向C点运动,问当t为何值时,四边形BPHE是平行四边形?当t取何值时,四边形PCFH是平行四边形?
【答案】(1)证明见解析;(2)20;(3)2秒
【解析】试题分析:(1)根据等腰三角形的三线合一可得出D为BC的中点,结合E、F分别为AB、AC的中点可得出DE和DF是△ABC的中位线,根据中位线的定义可得出DE∥AC、DF∥AB,即四边形AEDF是平行四边形,根据三角形中位线定义可得出DE=![]() AC、DF=
AC、DF=![]() AB,结合AB=AC即可得出DE=DF,从而得出四边形AEDF是菱形;
AB,结合AB=AC即可得出DE=DF,从而得出四边形AEDF是菱形;
(2)根据中位线的定义可得出EF的长度,根据菱形的面积公式可求出菱形AEDF的面积;
(3)由中位线的定义可得出EF∥BC,根据平行四边形的判定定理可得出关于t的一元一次方程,解之即可得出结论.
详解:(1)证明:∵AB=AC,AD⊥BC,
∴D为BC的中点.
∵E、F分别为AB、AC的中点,
∴DE和DF是△ABC的中位线,
∴DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形.
∵E,F分别为AB,AC的中点,AB=AC,
∴AE=AF,
∴四边形AEDF是菱形,
(2)解:∵EF为△ABC的中位线,
∴EF=![]() BC=5.
BC=5.
∵AD=8,AD⊥EF,
∴S菱形AEDF=![]() ADEF=
ADEF=![]() ×8×5=20.
×8×5=20.
(3)解:∵EF∥BC,
∴EH∥BP.
若四边形BPHE为平行四边形,则须EH=BP,
∴5﹣2t=3t,
解得:t=1,
∴当t=1秒时,四边形BPHE为平行四边形.
∵EF∥BC,
∴FH∥PC.
若四边形PCFH为平行四边形,则须FH=PC,
∴2t=10﹣3t,
解得:t=2,
∴当t=2秒时,四边形PCFH为平行四边形.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 事件“任意一个x(x为实数)值,x2是不确定事件”
B. 已知某篮球运动员投篮投中的概率为0.6,则他投十次一定投中6次
C. 为了了解我市各超市销售的速冻食品质量情况,适合采取普查的方式调查
D. 投掷一枚质地均匀的硬币10次,可能有5次正面向上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为了答谢顾客,凡在本超市购物的顾客,均可凭购物小票参与抽奖活动,奖品是三种瓶装饮料,它们分别是:绿茶(500ml)、红茶(500ml)和可乐(600ml),抽奖规则如下:①如图,是一个材质均匀可自由转动的转盘,转盘被等分成五个扇形区域,每个区域上分别写有“可”、“绿”、“乐”、“茶”、“红”字样;②参与一次抽奖活动的顾客可进行两次“有效随机转动”(当转动转盘,转盘停止后,可获得指针所指区域的字样,我们称这次转动为一次“有效随机转动”);③假设顾客转动转盘,转盘停止后,指针指向两区域的边界,顾客可以再转动转盘,直到转动为一次“有效随机转动”;④当顾客完成一次抽奖活动后,记下两次指针所指区域的两个字,只要这两个字和奖品名称的两个字相同(与字的顺序无关),便可获得相应奖品一瓶;不相同时,不能获得任何奖品.
根据以上规则,回答下列问题:
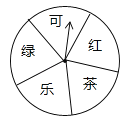
(1)求一次“有效随机转动”可获得“乐”字的概率;
(2)有一名顾客凭本超市的购物小票,参与了一次抽奖活动,请你用列表或树状图等方法,求该顾客经过两次“有效随机转动”后,获得一瓶可乐的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFMN的一边MN在边BC上,顶点E、F分别在AB、AC上,其中BC=24cm,高AD=12cm.
(1)求证:△AEF∽△ABC:
(2)求正方形EFMN的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标平面内,已知点![]() 的坐标
的坐标![]() ,点
,点![]() 位置如图所示,点
位置如图所示,点![]() 与点
与点![]() 关于原点对称。
关于原点对称。
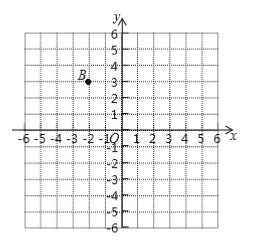
(1)在图中描出点![]() ;写出图中点
;写出图中点![]() 的坐标:______________,点
的坐标:______________,点![]() 的坐标:_______________;
的坐标:_______________;
(2)画出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ,并求出四边形
,并求出四边形![]() 的面积。
的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
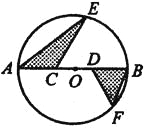
【题目】如图,半径为6cm 的⊙O中,C,D为直径AB 的三等分点,点E,F分别在AB两侧的半圆上,∠BCE =∠BDF = 60°,连结AE,BF.则图中两个阴影部分的面积和为 cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
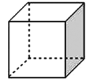
【题目】用一个平面去截正方体(如图),下列关于截面(截出的面)形状的结论:
①可能是锐角三角形;②可能是钝角三角形;
③可能是长方形;④可能是梯形.
其中正确结论的是______(填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com