
分析 设y=x2-2|x|-a,将方程解的情况转化成函数图象与x轴交点的问题,根据方程有4个实数根,结合函数图象即可得出关于a的一元一次不等式组,解不等式组即可得出结论.
解答 解:设y=x2-2|x|-a,
∵关于x的方程x2-2|x|=a有4个实数根,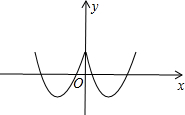
∴当x≥0时,y=x2-2x-a与x轴正半轴有两个不同的交点;x<0时,y=x2+2x-a与x轴负半轴有两个不同的交点(如图所示).
∴$\left\{\begin{array}{l}{-a>0}\\{△=(-2)^{2}-4×1×(-a)>0}\\{△={2}^{2}-4×1×(-a)>0}\end{array}\right.$,
解得:-1<a<0.
故答案为:-1<a<0.
点评 本题考查了根的判别式、数形结合以及解一元一次不等式组,解题的关键是利用数形结合得出关于a的一元一次不等式组.本题属于中档题,难度不大,利用数形结合来简化问题是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知函数y=ax2+bx+c的图象如图示,画出下列函数图象.
已知函数y=ax2+bx+c的图象如图示,画出下列函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在△ABC中,AB=AC,过AB延长线上一点D,作直线DE交BC于F,交AC于E,求证:$\frac{DF}{FE}=\frac{BD}{CE}$.
在△ABC中,AB=AC,过AB延长线上一点D,作直线DE交BC于F,交AC于E,求证:$\frac{DF}{FE}=\frac{BD}{CE}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 阅读下面材料:在数学课上,老师提出如下问题:
阅读下面材料:在数学课上,老师提出如下问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com