
【题目】如图,在锐角△ABC中,∠BAC=45°,AB=2,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是 . 
【答案】![]()
【解析】解:如图,作BH⊥AC,垂足为H,交AD于M′点,过M′点作M′N′⊥AB,垂足为N′, 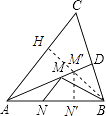
则BM′+M′N′为所求的最小值.
∵AD是∠BAC的平分线,
∴M′H=M′N′,
∴BH是点B到直线AC的最短距离(垂线段最短),
∵AB=2,∠BAC=45°,
∴BH=ABsin45°=2× ![]() =
= ![]() ,
,
∵BM+MN的最小值是BM′+M′N′=BM′+M′H=BH= ![]() .
.
故答案为: ![]() .
.
作BH⊥AC,垂足为H,交AD于M′点,过M′点作M′N′⊥AB,垂足为N′,则BM′+M′N′为所求的最小值,再根据AD是∠BAC的平分线可知M′H=M′N′,再由锐角三角函数的定义即可得出结论.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】第六次全国人口普查公布的数据表明,登记的全国人靠数量约为1 340 000 000人.这个数据用科学记数法表示为( )
A、134×107人B、13.4×108人
C、1.34×109人D、1.34×1010人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①“明天的降水概率为80%”是指明天有80%的时间在下雨;②连续抛一枚硬币50次,出现正面朝上的次数一定是25次( )
A. 只有①正确B. 只有②正确C. ①②都正确D. ①②都错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A超市在一次周年庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖机会,抽奖规则如下:将如图所示的图形转盘平均分成四个扇形,分别标上1,3,5,7四个数字,抽奖者连续转动转盘两次,当每次停止后指针所指扇形内的数为每次所得数(若指针指在分界处重转),当两次所得数字之和为2时,返现金20元,当两次所得数字之和为4时,返现金10元,当两次所得数字之和为6时,返现金5元.
(1)试用树状图或列表的方法,表示出王大妈这次抽奖中所有可能出现的结果.
(2)试求王大妈在参加这次抽奖活动中,能获得返现金的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
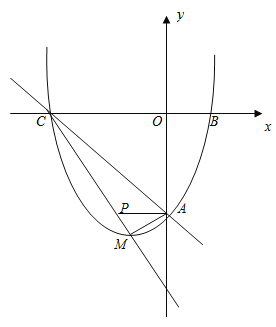
【题目】如图,已知抛物线y=ax2+bx+c与x轴交于点B,C,与直线AC:y=-x-6交y轴于点A,点M是抛物线的顶点,且横坐标为-2.
(1)求出抛物线的表达式.
(2)判断△ACM的形状并说明理由.
(3)直线CM交y轴于点F,在直线CM上是否存在一点P,使∠CMA=∠PAF,若存在,求出P的坐标,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com