
【题目】如图,已知AB=AC,AE=AF,BE与CF交于点D,则①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上,以上结论中,正确的是
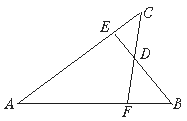
A. 只有①B. 只有②
C. 只有①和②D. ①②与③
科目:初中数学 来源: 题型:
【题目】“某工厂用如图甲所示的长方形和正方形纸板做成如图乙所示的 A、B 两种长方体形状的无盖纸盒.现 有正方形纸板 120 张,长方形纸板 360 张,刚好全部用完,问能做成多少个 A 型盒子?”则下列结论 正确的个数是( )

①甲同学:设 A 型盒子个数为 x 个,根据题意可得: 4x 3 ![]() 360
360
②乙同学:设 B 型盒中正方形纸板的个数为 m 个,根据题意可得: 3 ![]() 4(120 m) 360
4(120 m) 360
③A 型盒 72 个
④B 型盒中正方形纸板 48 个
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
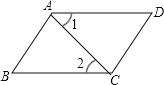
【题目】 根据题意,完成推理填空:如图,AB∥CD,∠1=∠2,试说明∠B=∠D.
解:∵∠1=∠2(已知)
∴ (內错角相等,两直线平行)
∴∠BAD+∠B=180°(两直线平行,同旁内角互补)
∵AB∥CD
∴ + =180°,
∴∠B=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
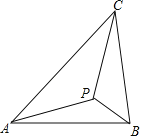
【题目】(2017湖南株洲)如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780﹣1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845﹣1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( )
A. 5 B. 4 C. 3+![]() D. 2+
D. 2+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).
(1)若m=6,求当P,E,B三点在同一直线上时对应的t的值.
(2)已知m满足:在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,求所有这样的m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
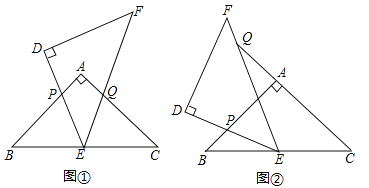
【题目】(2017甘肃省天水市)△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=2,CQ=9时BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
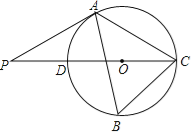
(1)求证:PA是⊙O的切线;
(2)若PD=![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
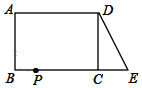
【题目】我们已经知道,有一个内角是直角的三角形是直角三角形.其中直角所在的两条边叫直角边,直角所对的边叫斜边(如图①所示).数学家已发现在一个直角三角形中,两个直角边边长的平方和等于斜边长的平方.如果设直角三角形的两条直角边长度分别是a和b,斜边长度是c,那么可以用数学语言表达:a2+b2=c2.已知,如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=3,连接DE.
(1)DE的长为 .
(2)动点P从点B出发,以每秒1个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒,求当t为何值时,△ABP和△DCE全等?
(3)若动点P从点B出发,以每秒1个单位的速度仅沿着BE向终点E运动,连接DP.设点P运动的时间为t秒,是否存在t,使△PDE为等腰三角形?若存在,请直接写出t的值;否则,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是关于
是关于![]() 的方程
的方程![]() 的一个实数根,并且这个方程的两个实数根恰好是等腰三角形
的一个实数根,并且这个方程的两个实数根恰好是等腰三角形![]() 的两条边长,则
的两条边长,则![]() 的周长为( )
的周长为( )
A. 6 B. 8 C. 10 D. 8或10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com