
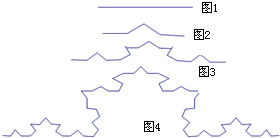
 若图1中的线段长为1,将此线段三等分,并以中间的一段为边作等边三角形,然后去掉这一段,得到图2称第1次操作,再将图2中的每一段类似变形,得到图3即第2次操作,按上述方法继续得到图4为第3次操作,则第4次操作后折线的总长度为$\frac{64}{27}$.
若图1中的线段长为1,将此线段三等分,并以中间的一段为边作等边三角形,然后去掉这一段,得到图2称第1次操作,再将图2中的每一段类似变形,得到图3即第2次操作,按上述方法继续得到图4为第3次操作,则第4次操作后折线的总长度为$\frac{64}{27}$. 分析 在图2中,折线的长度为:1+$\frac{1}{3}$=$\frac{4}{3}$;在图3中,折线的长度为:$\frac{4}{3}$+$\frac{4}{3}$×$\frac{1}{3}$=$\frac{16}{9}$;在图4中,折线的长度为:$\frac{16}{9}$+$\frac{16}{9}$×$\frac{1}{3}$=$\frac{64}{27}$,从而可求出折线的总长度.
解答 解:由题意得:在图2中,折线的长度为:1+$\frac{1}{3}$=$\frac{4}{3}$;
在图3中,折线的长度为:$\frac{4}{3}$+$\frac{4}{3}$×$\frac{1}{3}$=$\frac{16}{9}$;
在图4中,折线的长度为:$\frac{16}{9}$+$\frac{16}{9}$×$\frac{1}{3}$=$\frac{64}{27}$.
则第4次操作后折线的总长度为$\frac{64}{27}$+$\frac{64}{27}$×$\frac{1}{3}$=$\frac{256}{81}$.
点评 此题考查的知识点是图形数字的变化类问题,同时考查学生分析归纳问题的能力,其关键是读懂题意,找出规律解答.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
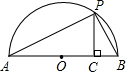 已知a、b是正实数,那么,$\frac{a+b}{2}$$≥\sqrt{ab}$是恒成立的.
已知a、b是正实数,那么,$\frac{a+b}{2}$$≥\sqrt{ab}$是恒成立的.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
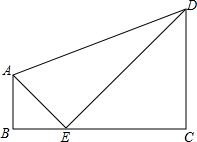 如图,已知直角梯形ABCD中,∠ABC=∠DCB=90°,点E在高上,且BE=AB=a,CE=CD=b,
如图,已知直角梯形ABCD中,∠ABC=∠DCB=90°,点E在高上,且BE=AB=a,CE=CD=b,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
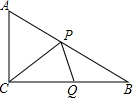 如图,Rt△ABC中,∠ACB=90°,CA=3cm,CB=4cm,设点P、Q为AB、CB上动点,它们分别从A、C同时出发向B点匀速移动,移动速度都为1cm/秒,移动时间为t秒(0≤t≤4),在整个移动过程中,
如图,Rt△ABC中,∠ACB=90°,CA=3cm,CB=4cm,设点P、Q为AB、CB上动点,它们分别从A、C同时出发向B点匀速移动,移动速度都为1cm/秒,移动时间为t秒(0≤t≤4),在整个移动过程中,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
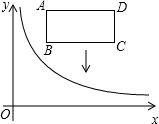 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$ (x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$ (x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 列方程或方程组解应用题:
列方程或方程组解应用题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com