
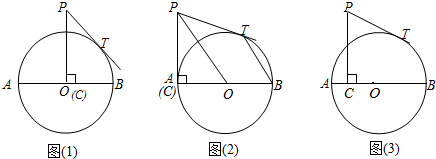
分析 (1)连接OT,根据题意,由勾股定理可得出PT的长;
(2)连接OT,则OP平分劣弧AT,则∠AOP=∠B,从而证出结论;
(3)设PC交⊙O于点D,延长线交⊙O于点E,由相交弦定理,可得出CD的长,再由切割线定理可得出y与x之间的关系式,进而求得y的最小值.
解答 (1) 解:如图(1),连接OT,
解:如图(1),连接OT,
∵PC=5,OT=4,
∴由勾股定理得,PT=$\sqrt{P{C^2}-O{T^2}}$=$\sqrt{25-16}$=3;
(2)证明:如图(2)连接OT,
∵PT,PC为⊙O的切线,
∴OP平分劣弧AT,
∴∠POA=∠POT,
∵∠AOT=2∠B,
∴∠AOP=∠B,
∴PO∥BT;
(3)解:如图(3),连接PO,PT
∵AB是⊙O的直径,AB=8,AC=x
∴CO=4-x;
又∵PC⊥AB
∴PO=$\sqrt{{{(4-x)}^2}+{5^2}}$
∴y=PT=$\sqrt{P{O^2}-O{T^2}}$=$\sqrt{{{(4-x)}^2}+{5^2}-{4^2}}$=$\sqrt{{x^2}-8x+25}$
∴y最小=$\sqrt{(x-4)^{2}+9}$=3.
点评 本题是一道圆综合题,考查了切线的性质、二次函数的最值以及勾股定理的内容,是中考压轴题,难度较大.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
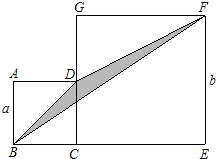 四边形ABCD和CEFG都是正方形,且正方形ABCD的边长为a,正方形CEFG的边长为b,连接BD,BF和DF后得到三角形BDF,请用含字母a和b的代数式表示三角形BDF的面积可表示为( )
四边形ABCD和CEFG都是正方形,且正方形ABCD的边长为a,正方形CEFG的边长为b,连接BD,BF和DF后得到三角形BDF,请用含字母a和b的代数式表示三角形BDF的面积可表示为( )| A. | ab | B. | $\frac{1}{2}$ab | C. | $\frac{1}{2}$b2 | D. | $\frac{1}{2}$a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
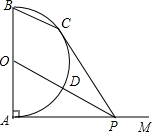 如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC.
如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,分别以Rt△ABC的直角边AC,斜边AB为边向△ABC外构造等边△ACD和等边△ABE,F为AB的中点,连接DF,EF,∠ACB=90°,∠ABC=30°.有下列四个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④$\frac{{S}_{△ACD}}{{S}_{四边形BCDE}}$=$\frac{1}{6}$.其中正确的结论是①②(填写正确结论的序号).
如图所示,分别以Rt△ABC的直角边AC,斜边AB为边向△ABC外构造等边△ACD和等边△ABE,F为AB的中点,连接DF,EF,∠ACB=90°,∠ABC=30°.有下列四个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④$\frac{{S}_{△ACD}}{{S}_{四边形BCDE}}$=$\frac{1}{6}$.其中正确的结论是①②(填写正确结论的序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
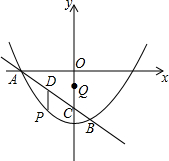 如图,已知抛物线y=ax2+c与直线$y=-\frac{3}{4}x-3$交于A,B两点,直线AB与y轴交于点C,点B的坐标为(1,$-\frac{15}{4}$),动点P在直线AB下方的抛物线上,动点Q在y轴上,动点D在线段AB上,且PD∥y轴.
如图,已知抛物线y=ax2+c与直线$y=-\frac{3}{4}x-3$交于A,B两点,直线AB与y轴交于点C,点B的坐标为(1,$-\frac{15}{4}$),动点P在直线AB下方的抛物线上,动点Q在y轴上,动点D在线段AB上,且PD∥y轴.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一块三角形纸板ABC,∠ACB=90°,AC=3,AB=5,把它置于平面直角坐标系中,AC∥y轴,BC∥x轴,顶点A,B恰好都在反比例函数y=$\frac{k}{x}$的图象上,AC,BC的延长线分别交x轴、y轴于D,E两点,设点C的坐标为(m,n).
一块三角形纸板ABC,∠ACB=90°,AC=3,AB=5,把它置于平面直角坐标系中,AC∥y轴,BC∥x轴,顶点A,B恰好都在反比例函数y=$\frac{k}{x}$的图象上,AC,BC的延长线分别交x轴、y轴于D,E两点,设点C的坐标为(m,n).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com