
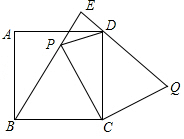
 如图,正方形ABCD中,AB=10,点P是正方形ABCD内的一点,PB=$\frac{25}{3}$,PB=PC,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ,延长BP交直线DQ于点E,则△EDP的面积为$\frac{17}{3}$.
如图,正方形ABCD中,AB=10,点P是正方形ABCD内的一点,PB=$\frac{25}{3}$,PB=PC,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ,延长BP交直线DQ于点E,则△EDP的面积为$\frac{17}{3}$. 分析 作PH⊥BC于H,CM⊥BE于M,CN⊥EQ于N.由△BCP≌△DCQ,推出∠CPM=∠Q,推出△CMP≌△CNQ,推出四边形EMCN是正方形,想办法求出PE、DE即可解决问题.
解答 解:如图,作PH⊥BC于H,CM⊥BE于M,CN⊥EQ于N.
∵四边形ABCD是正方形,
∴CB=CD,∠BCD=∠PCQ=90°,
∴∠BCD=∠PCQ,
∴∠BCP=∠DCQ,
在△BCP和△DCQ中,
$\left\{\begin{array}{l}{BC=CD}\\{∠BCP=∠DCQ}\\{CP=CQ}\end{array}\right.$,
∴△BCP≌△DCQ,
∴∠CPM=∠Q,
在△CMP和△CNQ中,
$\left\{\begin{array}{l}{∠CPM=∠Q}\\{∠CMP=∠CNQ=90°}\\{CP=CQ}\end{array}\right.$,
∴△CMP≌△CNQ,
∴CM=CN,∠PCM=∠QCN,
∴∠MCN=∠PCQ=90°,
∴∠MCN=∠CME=∠CNE=90°,
∴四边形EMCN是矩形,∵CM=CN,
∴四边形EMCN是正方形,
∵PB=PC,PH⊥BC,
∴BH=CH=5,
在Rt△PBH中,PH=$\sqrt{P{B}^{2}-B{H}^{2}}$=$\frac{20}{3}$,
∵S△PBC=$\frac{1}{2}$•PB•CM=$\frac{1}{2}$•BC•PH,
∴CM=CN=EM=EN=8,
在Rt△PCM中,PM=$\sqrt{P{C}^{2}-C{M}^{2}}$=$\frac{7}{3}$,
∴BM=6,
∴DN=6,PE=$\frac{17}{3}$,DE=2,
∴S△PDE=$\frac{1}{2}$•PE•DE=$\frac{17}{3}$,
故答案为$\frac{17}{3}$.
点评 本题考查旋转变换、正方形的性质和判定、全等三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,本题的突破点是证明四边形EMCN是正方形,属于中考填空题中的压轴题.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:解答题
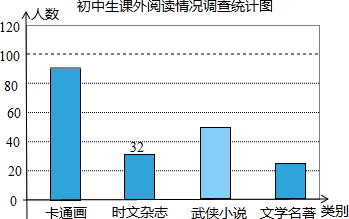 某校随机调查了部分学生,就“你最喜欢的图书类别”(只选一项)对学生课外阅读的情况作了调查统计,将调查结果统计后绘制成如下统计表和条形统计图,请根据统计图表提供的信息解答下列问题:
某校随机调查了部分学生,就“你最喜欢的图书类别”(只选一项)对学生课外阅读的情况作了调查统计,将调查结果统计后绘制成如下统计表和条形统计图,请根据统计图表提供的信息解答下列问题:| 种类 | 频数 | 频率 |
| 卡通画 | a | 0.45 |
| 时文杂志 | b | 0.16 |
| 武侠小说 | 50 | c |
| 文学名著 | d | e |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线l与x轴,y轴分别交于M,N两点,且OM=ON=3.
如图,直线l与x轴,y轴分别交于M,N两点,且OM=ON=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com