
����Ŀ��ij��λ�����ڲ���Ƹ������Աһ�����Լס��ҡ���������ѡ�˽����˱��Ժ�����������ԣ����˵IJ��Գɼ����±���ʾ��
������Ŀ | ���Գɼ����֣� | ||
�� | �� | �� | |
���� | 75 | 80 | 90 |
���� | 93 | 70 | 68 |
����¼�ó�����֯200��ְ������������ͶƱ�Ƽ��ķ�ʽ�����������飬���˵�Ʊ�ʣ�û����ȨƱ��ÿλְ��ֻ���Ƽ�1�ˣ���ͼ��ʾ��ÿ��һƱ����1�֣�
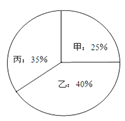
��1����������˵���������÷�.
��2���������������Ե�ƽ���ɼ�ȷ��¼����ѡ����ô˭����¼�ã���ȷ��0.01����
��3������ʵ����Ҫ����λ�����ԡ����ԡ���������������Ե÷ְ�4�U3�U3![]() �ı���ȷ�����˳ɼ�����ô˭����¼�ã�
�ı���ȷ�����˳ɼ�����ô˭����¼�ã�
���𰸡���1���ס��ҡ�������������÷ֱַ�Ϊ50�֡�80�֡�70��;��2���ҽ���¼�ã���3��������¼��.
���������������:��1����������ͳ��ͼ�е����ݼ�����üס��ҡ�������������÷֣�
��2������ƽ�����ĸ�����üס��ҡ�����ƽ���ɼ������бȽϣ�
��3�����ݼ�Ȩ�ɼ��ֱ�������˵ĸ��˳ɼ������бȽϣ�
ͨ���Ķ������ȡ��Ϣ���ٸ�����ĿҪ�����ƽ�������Ȩƽ�����ļ���.
�⣺��1���ס��ҡ�������������÷ֱַ�Ϊ50�֡�80�֡�70�֣�
��2����ƽ���ɼ�Ϊ![]() ���֣���
���֣���
�ҵ�ƽ���ɼ�Ϊ![]() ���֣���
���֣���
����ƽ���ɼ�Ϊ![]() ���֣���
���֣���
��Ϊ76.67��76.00��72.67�������ҽ���¼�ã�
��3����������ԡ����ԡ���������������Ե÷ְ�4�U3�U3![]() �ı���ȷ�����˳ɼ�����ô
�ı���ȷ�����˳ɼ�����ô
�ĸ��˳ɼ�Ϊ![]() ���֣���
���֣���
�ҵĸ��˳ɼ�Ϊ![]() ���֣���
���֣���
���ĸ��˳ɼ�Ϊ![]() ���֣���
���֣���
��Ϊ���ĸ��˳ɼ���ߣ����Ա�����¼��.


 ������ϰ�ο����뵥Ԫ���ϵ�д�
������ϰ�ο����뵥Ԫ���ϵ�д� �����Ծ���ĩ���100��ϵ�д�
�����Ծ���ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����䷽���ⷽ��x2��2x��6=0ʱ��ԭ����Ӧ����Ϊ�� ��
A.��x+1��2=7
B.��x��1��2=7
C.��x+2��2=10
D.��x��2��2=10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����⣺��ͼ���߶�AC��������D��B��E���㣬���е�BΪ�߶�AC���е㣬AD=BE����DE=4�����߶�AC�ij��� ![]()
�벹ȫ���½����̣�
�⣺��D��B��E�����������߶�AC�ϣ�
��DE=+BE��
��AD=BE��
��DE=DB+=AB��
��DE=4��
��AB=4��
�� ��
��AC=2AB= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Ǽ�������ǣ� ��
A. �����εĽ�ƽ���߶����������ڲ� B. �����ε������߶����������ڲ�
C. �����ε��������߶����������ڲ� D. �����ε�������ƽ�����ཻ��һ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����OΪֱ��AB��һ�㣬��AOC=110�㣬OMƽ�֡�AOC����MON=90�� 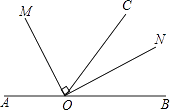
��1�����BOM�Ķ�����
��2��ON�ǡ�BOC�Ľ�ƽ��������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ԼΪ27100ƽ�������27100������ÿ�ѧ��������ʾΪ��������
A. 27.1��102 B. 2.71��103 C. 2.71��104 D. 0.271��105
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
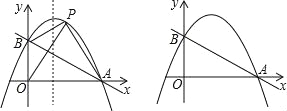
����Ŀ����ͼ��ֱ��y=��![]() x+1��x�ύ�ڵ�A����y�ύ�ڵ�B��������y=��x2+bx+c����A��B���㣮
x+1��x�ύ�ڵ�A����y�ύ�ڵ�B��������y=��x2+bx+c����A��B���㣮
��1���������ߵĽ���ʽ��
��2����P�ǵ�һ�����������ϵ�һ�㣬����PA��PB��PO������POA���������POB�����![]() ����
����
�����P�����ꣻ
����QΪ�����߶Գ�����һ�㣬��ֱ��д��QP+QA����Сֵ��
��3����MΪֱ��AB�ϵĶ��㣬��NΪ�������ϵĶ��㣬���Ե�O��B��M��NΪ������ı�����ƽ���ı���ʱ����ֱ��д����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾������ҵ�������շ����£���Ʒ���ӹ��ѹ�1000Ԫ������ÿ����ȡ���Ϸ�4Ԫ�������շ�y�����������IJ���x�ĺ�����ϵʽΪ ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com