
分析 (1)把x=-1代入原方程得到关于m的一元二次方程,然后解关于m的一元二次方程即可;
(2)进行判别式的值,利用完全平方公式变形得到△=4(m+1)2+49,然后利用非负数的性质可判断△>0,从而根据判别式的意义可判断方程根的情况.
解答 (1)解:把x=-1代入x2-5x-m2-2m-7=0得1+5-m2-2m-7=0,解得m1=m2=-1,
即m的值为1;
(2)证明:△=(-5)2-4(-m2-2m-7)
=4(m+1)2+49,
∵4(m+1)2≥0
∴△>0,
∴方程都有两个不相等的实数根.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.


科目:初中数学 来源: 题型:解答题
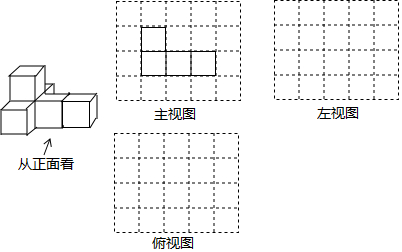
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
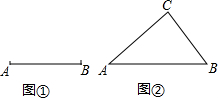 定义:如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“奇异三角形”,这条中线为“奇异中线”.
定义:如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“奇异三角形”,这条中线为“奇异中线”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
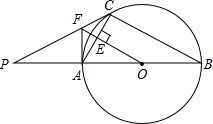 如图,C是以AB为直径的⊙O上一点,过O作OE⊥AC于点E,过点A作⊙O的切线交OE的延长线于点F,连接CF并延长交BA的延长线于点P.
如图,C是以AB为直径的⊙O上一点,过O作OE⊥AC于点E,过点A作⊙O的切线交OE的延长线于点F,连接CF并延长交BA的延长线于点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com