
分析 利用配方法求二次函数的最值.
解答 解:y=2x2+3mx+2m=2(x+$\frac{3}{4}$m)2-$\frac{3}{8}$m2+2m.
因为函数y=2x2+3mx+2m的最小值为$\frac{8}{9}$.
所以-$\frac{3}{8}$m2+2m=$\frac{8}{9}$,
解得m=$\frac{24±8\sqrt{6}}{9}$.
故答案是:$\frac{24±8\sqrt{6}}{9}$.
点评 本题考查了二次函数的最值.当a>0时,抛物线在对称轴左侧,y随x的增大而减少;在对称轴右侧,y随x的增大而增大,因为图象有最低点,所以函数有最小值,当x=-$\frac{b}{2a}$时,y=$\frac{4ac-{b}^{2}}{4a}$.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
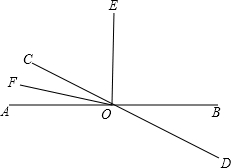 如图,已知直线AB,CD相交于点O,OE,OF为射线,∠AOE=90°,OF平分∠AOC,∠AOF+∠BOD=51°,求:
如图,已知直线AB,CD相交于点O,OE,OF为射线,∠AOE=90°,OF平分∠AOC,∠AOF+∠BOD=51°,求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
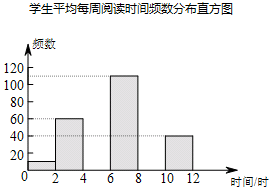 阅读下列材料:
阅读下列材料:| 平均每周阅读时间x(时) | 频数 | 频率 |
| 0≤x<2 | 10 | 0.025 |
| 2≤x<4 | 60 | 0.150 |
| 4≤x<6 | a | 0.200 |
| 6≤x<8 | 110 | b |
| 8≤x<10 | 100 | 0.250 |
| 10≤x<12 | 40 | 0.100 |
| 合计 | 400 | 1.000 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
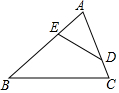 如图,在△ABC中,D,E分别是AC和AB上的点,AD=3cm,AC=4cm,AE=2cm,且$\frac{AD}{AB}$=$\frac{AE}{AC}$,则AB=6cm,BE=4cm.
如图,在△ABC中,D,E分别是AC和AB上的点,AD=3cm,AC=4cm,AE=2cm,且$\frac{AD}{AB}$=$\frac{AE}{AC}$,则AB=6cm,BE=4cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
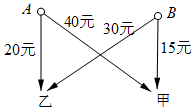 我县黄泛区农场有A、B两个果园,分别收获水果380件,320件,现需把这些水果全部运往甲、乙两个销售点,每件运费如图所示.现甲销售点需水果400件,乙销售点需水果300件.
我县黄泛区农场有A、B两个果园,分别收获水果380件,320件,现需把这些水果全部运往甲、乙两个销售点,每件运费如图所示.现甲销售点需水果400件,乙销售点需水果300件.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
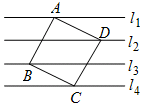 如图,已知直线l1∥l2∥l3∥l4,且相邻两条平行直线间的距离都是d,如果正方形ABCD的四个顶点分别在四条直线上,且面积都是1,则d=$\frac{\sqrt{5}}{5}$.
如图,已知直线l1∥l2∥l3∥l4,且相邻两条平行直线间的距离都是d,如果正方形ABCD的四个顶点分别在四条直线上,且面积都是1,则d=$\frac{\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
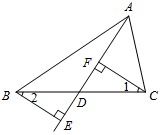 完成下面的证明:
完成下面的证明:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com