
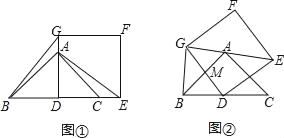
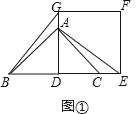
【题目】如图①,AD为等腰直角△ABC的高,点A和点C分别在正方形DEFG的边DG和DE上,连接BG、AE.
(1)求证:BG=AE;
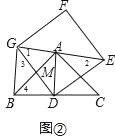
(2)将正方形DEFG绕点D旋转,当线段EG经过点A时,(如图②所示)
①求证:BG⊥GE;
②设DG与AB交于点M,若AG=6,AE=8,求DM的长.
【答案】(1)证明见解析;(2)①证明见解析;②DM=![]() ,
,
【解析】试题分析:(1)如图①,根据等腰直角三角形的性质得AD=BD,再根据正方形的性质得∠GDE=90°,DG=DE,则可根据“SAS“判断△BDG≌△ADE,于是得到BG=AE;
(2)①如图②,先判断△DEG为等腰直角三角形得到∠1=∠2=45°,再由△BDG≌△ADE得到∠3=∠2=45°,则可得∠BGE=90°,所以BG⊥GE;
②由AG=6,则AE=8,即GE=14,利用等腰直角三角形的性质得DG=![]() GE=7
GE=7![]() ,由(1)的结论得BG=AE=8,则根据勾股定理得AB=10,接着由△ABD为等腰直角三角形得到∠4=45°,BD=
,由(1)的结论得BG=AE=8,则根据勾股定理得AB=10,接着由△ABD为等腰直角三角形得到∠4=45°,BD=![]() AB=5
AB=5![]() ,然后证明△DBM∽△DGB,则利用相似比可计算出DM;
,然后证明△DBM∽△DGB,则利用相似比可计算出DM;
试题解析:
(1)证明:如图①,
∵AD为等腰直角△ABC的高,
∴AD=BD,
∵四边形DEFG为正方形,
∴∠GDE=90°,DG=DE,
在△BDG和△ADE中
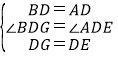 ,
,
∴△BDG≌△ADE,
∴BG=AE;
(2)①证明:如图②,
∵四边形DEFG为正方形,
∴△DEG为等腰直角三角形,
∴∠1=∠2=45°,
由(1)得△BDG≌△ADE,
∴∠3=∠2=45°,
∴∠1+∠3=45°+45°=90°,即∠BGE=90°,
∴BG⊥GE;
②解:∵AG=6,则AE=8,即GE=14,
∴DG=![]() GE=7
GE=7![]() ,
,
∵△BDG≌△ADE,
∴BG=AE=8,
在Rt△BGA中,AB=![]() =10,
=10,
∵△ABD为等腰直角三角形,
∴∠4=45°,BD=![]() AB=5
AB=5![]() ,
,
∴∠3=∠4,
而∠BDM=∠GDB,
∴△DBM∽△DGB,
∴BD:DG=DM:BD,即 5![]() :7
:7![]() =DM:5
=DM:5![]() ,
,
∴DM=![]() ,
,


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
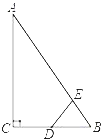
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t≤8),连接DE,当△BDE是直角三角形时,t的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
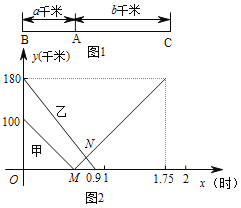
【题目】如图1所示,已知温沪动车铁路上有A、B、C三站,B、C两地相距 ![]() 千米,甲、乙两列动车分别从B、C两地同时沿铁路匀速相向出发向终点C、B站而行,甲、乙两动车离A地的距离
千米,甲、乙两列动车分别从B、C两地同时沿铁路匀速相向出发向终点C、B站而行,甲、乙两动车离A地的距离 ![]() (千米)与行驶时间表
(千米)与行驶时间表 ![]() (时)的关系如图2所示,根据图象,解答以下问题:
(时)的关系如图2所示,根据图象,解答以下问题:
(1) 填空:路程 ![]() ________________,路程
________________,路程 ![]() ________________,点
________________,点 ![]() 的坐标为________________.
的坐标为________________.
(2) 求动车甲离A地的距离 ![]() 与行驶时间
与行驶时间 ![]() 之间的函数关系式.
之间的函数关系式.
(3) 补全动车乙的大致的函数图象.(直接画出图象)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在下列横线上用含有a,b的代数式表示相应图形的面积.
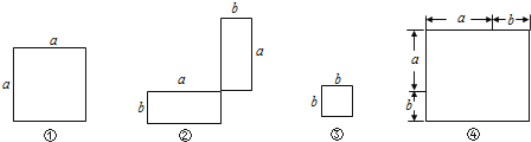
① ; ② ; ③ ; ④ .
(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表示: ;
(3)利用(2)的结论计算992+2×99×1+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,E、F分别是AB、CD的中点,AF与DE相交于点G,CE与BF相交于点H.
(1)求证:四边形EHFG是平行四边形;
(2)□ABCD应满足什么条件时,四边形EHFG是矩形?并说明理由;
(3)□ABCD应满足什么条件时,四边形EHFG是正方形?(不要说明理由).

查看答案和解析>>
科目:初中数学 来源: 题型:
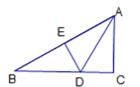
【题目】如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠BAC,DE⊥AB于E,有下列结论:①DE=DC;②∠BDE=∠ADC;③AB=2AC;④图中共有两对全等三角形.其中正确的是:____________(填序号即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
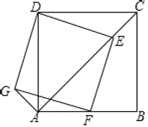
【题目】如图,正方形ABCD中,AB=4,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED,交AB于点F,以DE、EF为邻边作矩形DEFG,连接AG.
(1)求证:矩形DEFG是正方形;
(2)求AG+AE的值;
(3)若F恰为AB中点,连接DF交AC于点M,请直接写出ME的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校决定对学生感兴趣的球类项目(A:足球,B:篮球,C:排球,D:羽毛球,E:乒乓球)进行问卷调查,学生可根据自己的喜好选修一门,李老师对某班全班同学的选课情况进行统计后,制成了两幅不完整的统计图(如图).

(1)该班学生人数有 人;
(2)将条形统计图补充完整;
(3)若该校共有学生3500名,请估计有多少人选修足球?
(4)该班班委5人中,1人选修篮球,3人选修足球,1人选修排球,李老师要从这5人中任选2人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
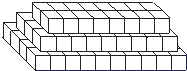
【题目】探索、研究:仪器箱按如图方式堆放(自下而上依次为第1层、第2层、…),受堆放条件限制,堆放时应符合下列条件:每层堆放仪器箱的个数a![]() 与层数n之间满足关系式a
与层数n之间满足关系式a![]() =n32n+247,1n<16,n为整数。
=n32n+247,1n<16,n为整数。
(1)例如,当n=2时,a![]() =232×2+247=187,则a
=232×2+247=187,则a![]() =___,a
=___,a![]() =___;
=___;
(2)第n层比第(n+1)层多堆放多少个仪器箱;(用含n的代数式表示)
(3)假设堆放时上层仪器箱的总重量会对下一层仪器箱产生同样大小的压力,压力单位是牛顿,设每个仪器箱重54 牛顿,每个仪器箱能承受的最大压力为160牛顿,并且堆放时每个仪器箱承受的压力是均匀的。
①若仪器箱仅堆放第1、2两层,求第1层中每个仪器箱承受的平均压力;
②在确保仪器箱不被损坏的情况下,仪器箱最多可以堆放几层?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com