
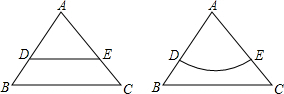
 如果是两个全等的等边三角形ABC,平行于BC的线段DE与以点A为圆心的$\widehat{DE}$把△ABC的面积分成相等的两部分,则线段DE的长小于$\widehat{DE}$的长.(填“大于”“小于”或“等于”)
如果是两个全等的等边三角形ABC,平行于BC的线段DE与以点A为圆心的$\widehat{DE}$把△ABC的面积分成相等的两部分,则线段DE的长小于$\widehat{DE}$的长.(填“大于”“小于”或“等于”) 分析 根据等边三角形的性质得出DE和$\widehat{DE}$的长度进行比较即可.
解答 解:如图1,设等边△ABC的边长为a,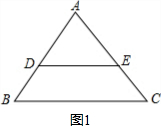
∵DE∥AB,
∴△ABC∽△ADE,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{2}$=($\frac{DE}{BC}$)2,
∴DE=$\frac{\sqrt{2}}{2}$a,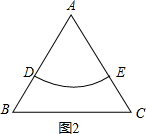
如图2,∵△AB是等边三角形,
∴∠A=60°,
∵$\widehat{DE}$把△ABC的面积分成面积相等的两部分,
∴$\frac{60π•(AD)^{2}}{360}$=$\frac{1}{2}$×a×$\frac{\sqrt{3}}{2}$a,
解得:AD2=$\frac{3\sqrt{3}{a}^{2}}{2π}$,
所以$\widehat{DE}$=$\frac{60π\sqrt{\frac{3\sqrt{3}{a}^{2}}{2π}}}{180}=\frac{\sqrt{6\sqrt{3}π}}{6}a$,
因为$(\frac{\sqrt{2}}{2})^{2}=\frac{1}{2}$,$(\frac{\sqrt{6\sqrt{3}π}}{6})^{2}=\frac{6\sqrt{3}π}{36}≈0.9$,
所以线段DE的长小于$\widehat{DE}$的长,
故答案为:小于.
点评 此题考查等边三角形的性质,关键是根据等边三角形的性质得出DE和$\widehat{DE}$的长度.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
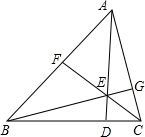 如图,在△ABC中,AD、BG、CF交于点E,则$\frac{EF}{CF}$+$\frac{EG}{BG}$+$\frac{ED}{AD}$=1.
如图,在△ABC中,AD、BG、CF交于点E,则$\frac{EF}{CF}$+$\frac{EG}{BG}$+$\frac{ED}{AD}$=1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-a2)3=a6 | B. | (a+b)2=a2+b2 | C. | $\root{3}{-64}$=-4 | D. | 5$\sqrt{5}$-$\sqrt{5}$=4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
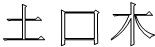 汉字是世界上最古老的文字之一,字形结构体现人类追求均衡对称、和谐稳定的天性,如图,三个汉字可以看成是轴对称图形.
汉字是世界上最古老的文字之一,字形结构体现人类追求均衡对称、和谐稳定的天性,如图,三个汉字可以看成是轴对称图形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com