
分析 根据∠A为锐角或∠D为锐角分情况进行讨论,由?ABCD的周长为18,DE⊥直线BC,DF⊥直线AB,垂足分别为E、F,且DE=3,DF=4,构造方程求解即可求得答案.
解答  解:对于平行四边形ABCD有两种情况:
解:对于平行四边形ABCD有两种情况:
当∠A为锐角时,如图1,
设BC=a,AB=b,
∵平行四边形ABCD,DE⊥AB,DF⊥BC,
∴AB×DE=BC×DF,AB=CD,BC=DA,
又∵DE=3,DF=4,
∴3a=4b,
∵平行四边形ABCD的周长为28,
∴2(a+b)=28,
∴a+b=14,
则$\left\{\begin{array}{l}{3a=4b①}\\{a+b=14②}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=8}\\{b=6}\end{array}\right.$,
∴BC=8,AB=6,
∴AB=CD=6,AD=BC=8,
∴在Rt△ADE中,CE=3$\sqrt{3}$,
∴BE=BC-CE=8-3$\sqrt{3}$,
∴在Rt△ADF中,AF=4$\sqrt{3}$,
∵F点在AB的延长线上,
∴BF=AF-AB=4$\sqrt{3}$-6,
∴BE+BF=(8-3$\sqrt{3}$)+(4$\sqrt{3}$-6)=2+$\sqrt{3}$,
当∠D为锐角时,如图2,
设BC=a,AB=b,
∵平行四边形ABCD,DE⊥AB,DF⊥BC,
∴AB×DE=BC×DF,AB=CD,BC=DA,
又∵DE=3,DF=4,
∴3a=4b,
∵平行四边形ABCD的周长为28,
∴2(a+b)=28,
∴a+b=14,
解方程组$\left\{\begin{array}{l}{3a=4b①}\\{a+b=14②}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=8}\\{b=6}\end{array}\right.$,
∴BC=8,AB=6,
∴AB=CD=6,AD=BC=8,
∴在Rt△ADE中,CE=3$\sqrt{3}$,
∴BE=BC+CE=8+3$\sqrt{3}$,
∴在Rt△ADF中,AF=4$\sqrt{3}$,
∵F点在AB的延长线上,
∴BF=AF+AB=4$\sqrt{3}$+6,
∴BE+BF=(8+3$\sqrt{3}$)+(4$\sqrt{3}$+6)=14+7$\sqrt{3}$,
故答案为:2+$\sqrt{3}$或14+7$\sqrt{3}$.
点评 本题主要考查平行四边形的性质,勾股定理,合并同类二次根式等知识点,关键在于根据∠A为锐角或∠D为锐角分情况进行讨论,根据平行四边形的面积公式和周长定理正确的列出方程组,并认真的求解,推出AB和BC的长度,熟练运用数形结合的思想进行求解.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
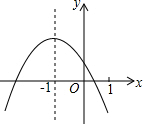 如图是抛物线y=ax2+bx+c的图象,则下列说法正确的有( )个.
如图是抛物线y=ax2+bx+c的图象,则下列说法正确的有( )个.| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com