
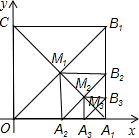
 如图,在平面直角坐标系中,边长为1的正方形OA1B1C的对角线A1C和OB1交于点M1;以A1M1为对角线作第二个正方形A2A1B2M1,对角线A1M1和A2B2交于点M2;以A1M2为对角线作第三个正方形A3A1B3M2,对角线A1M2和A3B3交于点M3;…依此类推,这样作的第n个正方形对角线交点Mn的坐标是($\frac{{2}^{n}-1}{{2}^{n}}$,$\frac{1}{{2}^{n}}$).
如图,在平面直角坐标系中,边长为1的正方形OA1B1C的对角线A1C和OB1交于点M1;以A1M1为对角线作第二个正方形A2A1B2M1,对角线A1M1和A2B2交于点M2;以A1M2为对角线作第三个正方形A3A1B3M2,对角线A1M2和A3B3交于点M3;…依此类推,这样作的第n个正方形对角线交点Mn的坐标是($\frac{{2}^{n}-1}{{2}^{n}}$,$\frac{1}{{2}^{n}}$). 分析 根据正方形的性质找出M1、M2、M3的坐标,根据其横纵坐标之间的关系即可找出点Mn的坐标为($\frac{{2}^{n}-1}{{2}^{n}}$,$\frac{1}{{2}^{n}}$),此题得解.
解答 解:∵正方形OA1B1C的边长为1,对角线A1C和OB1交于点M1,
∴点M1($\frac{1}{2}$,$\frac{1}{2}$);
∵以A1M1为对角线作第二个正方形A2A1B2M1,对角线A1M1和A2B2交于点M2,
∴点M2($\frac{3}{4}$,$\frac{1}{4}$);
∵以A1M2为对角线作第三个正方形A3A1B3M2,对角线A1M2和A3B3交于点M3,
∴M3($\frac{7}{8}$,$\frac{1}{8}$).
∵$\frac{1}{2}$=1-$\frac{1}{2}$,$\frac{3}{4}$=1-$\frac{1}{4}$,$\frac{1}{4}$=$\frac{1}{{2}^{2}}$,$\frac{7}{8}$=1-$\frac{1}{8}$,$\frac{1}{8}$=$\frac{1}{{2}^{3}}$,
∴Mn($\frac{{2}^{n}-1}{{2}^{n}}$,$\frac{1}{{2}^{n}}$).
故答案为:($\frac{{2}^{n}-1}{{2}^{n}}$,$\frac{1}{{2}^{n}}$).
点评 本题考查了规律型中点的坐标以及正方形的性质,根据部分点Mn的坐标的特点找出变化规律“Mn($\frac{{2}^{n}-1}{{2}^{n}}$,$\frac{1}{{2}^{n}}$)”是解题的关键.


科目:初中数学 来源: 题型:选择题
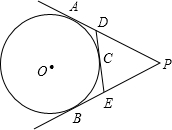 如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则△PDE的周长为( )
如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则△PDE的周长为( )| A. | 16cm | B. | 14cm | C. | 12cm | D. | 8cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
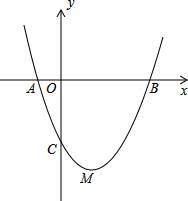 如图,在直角坐标系中,抛物线y=x2+bx-3与x轴交于A、B两点,与y轴于点C,顶点为M,已知A(-1,0).
如图,在直角坐标系中,抛物线y=x2+bx-3与x轴交于A、B两点,与y轴于点C,顶点为M,已知A(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com