
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:解答题
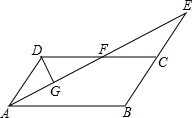 如图,在平行四边形ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F.
如图,在平行四边形ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
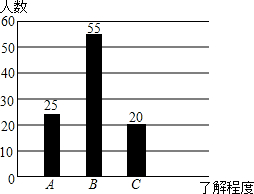 某中学组织学生开展社会实践活动,调查某社区居民对消防知识的了解程度(A:特别熟悉,B:有所了解,C:不知道),在该社区随机抽取了100名居民进行问卷调查,将调查结果制成如图所示的统计图,根据统计图解答下列问题:
某中学组织学生开展社会实践活动,调查某社区居民对消防知识的了解程度(A:特别熟悉,B:有所了解,C:不知道),在该社区随机抽取了100名居民进行问卷调查,将调查结果制成如图所示的统计图,根据统计图解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 总体 | B. | 样本 | C. | 个体 | D. | 样本容量 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
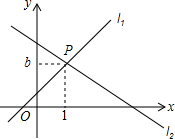 如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).
如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com