
【题目】小明四等分弧AB,他的作法如下:
①连接AB(如图);作AB的垂直平分线CD交弧AB于点M,交AB于点T;
②分别作AT,TB的垂直平分线EF,GH,交弧AB于N,P两点,则N,M,P三点把弧AB四等分。你认为小明的作法是否正确: , 理由是。
【答案】不正确;理由是:如图,连结AN并延长,交CD于J,连结MN,设EF与AB交于I.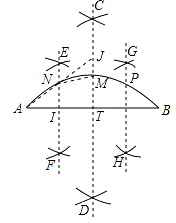 由作法可知,EF∥CD,AI=IT,∴AN=NJ,∵∠NMJ>∠NJM,∴NJ>MN,∴AN>MN,∴弦AN与MN不相等,则
由作法可知,EF∥CD,AI=IT,∴AN=NJ,∵∠NMJ>∠NJM,∴NJ>MN,∴AN>MN,∴弦AN与MN不相等,则 ![]() .
.
【解析】此题是将弧AB四等分,不是将弦AB四等分,根据圆心角、弧、弦的关系定理可知则弧AN≠弧MN,此题应根据垂径定理作图。
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对圆心角、弧、弦的关系的理解,了解在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,长方形纸片ABCD的长AD=9cm,宽AB=3cm,将其折叠,使点D与点B重合.
求:(1)折叠后DE的长;(2)以折痕EF为边的正方形面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的切线,B为切点,AO的延长线交⊙O于点C,连接BC,如果∠A=30°,AB=2 ![]() ,那么AC的长等于( )
,那么AC的长等于( )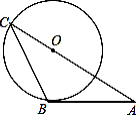
A.4
B.6
C.4 ![]()
D.6 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的任意一动点,点
边上的任意一动点,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,直线
对称,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
(1)求![]() 边上的高;
边上的高;
(2)当![]() 为何值时,△
为何值时,△![]() 与△
与△![]() 重叠部分的面积最大,并求出最大值;
重叠部分的面积最大,并求出最大值;
(3)连接![]() ,当
,当![]() 为直角三角形时,求
为直角三角形时,求![]() 的度数.
的度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级一班小张陪妈妈到水果市场购买水果,在一个水果摊前听到妈妈与售货员的对话:
妈妈:“售货员同志,请帮我买些上次梨.”
售货员:“大妈,您上次买的那种梨都卖完了,我们还没来得及进货,我建议这次您买些新进的苹果,价格比梨贵一点,不过苹果的营养价值更高.”
妈妈:“好,你们的服务态度和服务质量我很满意,这次我照上次一样,也买30元钱的苹果吧.”回家后对照前后两次的电脑小票,小张发现:每千克苹果的单价价是梨的单价的1.5倍,苹果的重量比梨轻2.5千克.
小张根据上面的对话和发票,求出了梨和苹果的单价,你知道梨和苹果的单价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在R t△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
(1)动手操作:利用尺规作,以AB边上一点O为圆心,过A,D两点作⊙O,与AB的另一个交点为E,与AC的另一个交点为F(不写作法,保留作图痕迹),再判断直线BC与⊙O的位置关系,并说明理由。
(2)若∠BAC=60度,CD= ![]() ,求线段BD、BE与劣弧DE所围成的图形面积.(结果保留根号和
,求线段BD、BE与劣弧DE所围成的图形面积.(结果保留根号和 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)光线从空气中射入水中会产生折射现象,同时光线从水中射入空气中也会产生折射现象,如图1,光线a从空气中射入水中,再从水中射入空气中,形成光线b,根据光学知识有∠1=∠2,∠3=∠4,请判断光线a与光线b是否平行,并说明理由;
(2)如图2,直线EF上有两点A、C,分别引两条射线AB、CD.已知∠BAF=150°,∠DCF=80°,射线AB、CD分别绕点A、点C以1度/秒和3度/秒的速度同时顺时针转动,设时间为t秒,当射线CD转动一周时,两条射线同时停止.则当直线CD与直线AB互相垂直时,t= 秒.
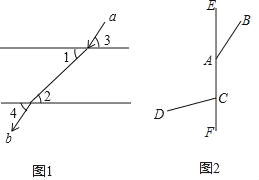
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com