Question

如图，已知：在ΔABC中，AB=AC，AD⊥BC，垂足为D，AN是ΔABC外角∠CAM的平分线，CE⊥AN，垂足为E．求证：四边形ADCE是矩形．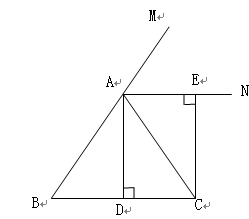

Answer 1

见解析

解析试题分析：由AB=AC，AD⊥BC，根据“三线合一”可得AD平分∠BAC，即∠DAC=∠BAC，再根据AN平分∠CAM，可得∠NAC=∠CAM，从而得到∠DAN=90°，再有CE⊥AN，AD⊥BC即可证得结论。
在△ABC中，AB=AC，AD⊥BC
∴AD平分∠BAC
∴∠DAC=∠BAC
又∵AN是ΔABC外角∠CAM的平分线
∴∠NAC=∠CAM
∴∠DAC+∠NAC=(∠BAC+∠CAM)=90°
即∠DAN=90°
又∵CE⊥AN，AD⊥BC
∴∠ADC=∠AEC=90°
∴∠ADC=∠AEC=∠DAN = 90°
∴四边形ADCE是矩形．
考点：本题考查的是等腰三角形的性质，角平分线的性质，矩形的判定
点评：解答本题的关键是运用“三线合一”及角平分线的性质得到∠DAN=90°。