
【题目】有一人患了流感,经过两轮传染后共有100人患了流感,每轮传染中平均一个人传染的人数x满足的方程为( )
A.1+x+x(1+x)=100
B.x(1+x)=100
C.1+x+x2=100
D.x2=100
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
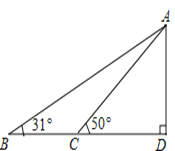
【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m)
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为
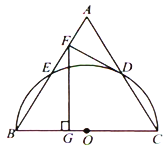
A. 4 B. ![]() C. 6 D.
C. 6 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m)
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与双曲线
与双曲线![]() 全相交于点A、B,且抛物线经过坐标原点,点
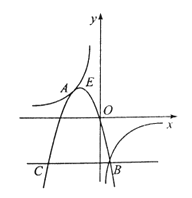
全相交于点A、B,且抛物线经过坐标原点,点![]() 的坐标为(一2,2),点B在第四象限内.过点B作直线BC//x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍.记抛物线顶点为E.
的坐标为(一2,2),点B在第四象限内.过点B作直线BC//x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍.记抛物线顶点为E.
(1)求双曲线和抛物线的解析式;
(2)计算![]() 与
与![]() 的面积;
的面积;
(3)在抛物线上是否存在点D,使![]() 的面积等于
的面积等于![]() 的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由.
的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com