
【题目】如图,已知抛物线与x交于A(﹣1,0)、E(3,0)两点,与y轴交于点B(0,3).
(1)求抛物线的解析式;
(2)设抛物线顶点为D,求四边形AEDB的面积.
【答案】
(1)
解:设抛物线的解析式为:y=a(x+1)(x﹣3),则有:
a(0+1)(0﹣3)=3,a=﹣1;
∴抛物线的解析式为:y=﹣x2+2x+3
(2)
解:由(1)知:y=﹣x2+2x+3=﹣(x﹣1)2+4,
即D(1,4);
过D作DF⊥x轴于F;
S四边形AEDB=S△AOB+S△DEF+S梯形BOFD= ![]() ×1×3+
×1×3+ ![]() ×2×4+
×2×4+ ![]() ×(3+4)×1=9;
×(3+4)×1=9;
即四边形AEDB的面积为9.

【解析】(1)已知了抛物线图象上的三点坐标,可用待定系数法求出抛物线的解析式;(2)根据抛物线的解析式,易求得抛物线顶点D的坐标;过D作DF⊥x轴于F,那么四边形AEDB的面积就可以由△AOB、△DEF、梯形BOFD的面积和求得.
【考点精析】认真审题,首先需要了解二次函数的图象(二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点),还要掌握二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小)的相关知识才是答题的关键.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
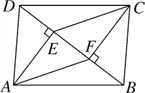
【题目】四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为点E,F.
(1)求证:△ADE≌△CBF;
(2)若AC与BD相交于点O,求证:AO=CO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA= ![]() .
. 
(1)在图中,求作△ABO的外接圆(尺规作图,不写作法但需保留作图痕迹);
(2)求点B的坐标与cos∠BAO的值;
(3)若A,O位置不变,将点B沿x轴向右平移使得△ABO为等腰三角形,请求出平移后点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
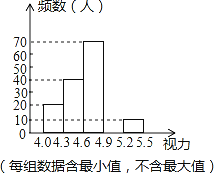
【题目】某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
(1)在频数分布表中,a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,数轴被折成90°,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字2所对应的点与数轴上的数3所对应的点重合,数轴固定,圆紧贴数轴沿着数轴的正方向滚动,那么数轴上的数2018将与圆周上的数字________重合.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有下列5个结论,①abc<0; ②2a+b=0;③b2﹣4ac<0;④a+b+c>0;⑤a﹣b+c<0.其中正确的结论有(填序号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,等边△ABC中,AD是BC边上的中线,根据等腰三角形的“三线合一”特性,AD平分∠BAC,且AD⊥BC,则有∠BAD=30°,BD=CD=![]() AB.于是可得出结论“直角三角形中, 30°角所对的直角边等于斜边的一半”.
AB.于是可得出结论“直角三角形中, 30°角所对的直角边等于斜边的一半”.
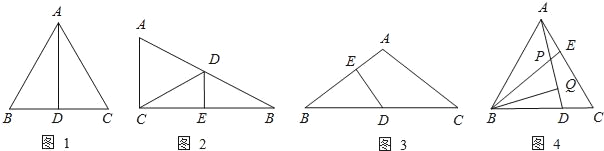
请根据从上面材料中所得到的信息解答下列问题:
(1)如图2所示,在△ABC中,∠ACB=90°,BC的垂直平分线交AB于点D,垂足为E,当BD=5cm,∠B=30°时,△ACD的周长= .
(2)如图3所示,在△ABC中,AB=AC,∠A=120°,D是BC的中点,DE⊥AB,垂足为E,那么BE:EA= .
(3)如图4所示,在等边△ABC中,D、E分别是BC、AC上的点,且AE=DC,AD、BE交于点P,作BQ⊥AD于Q,若BP=2,求BQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司招聘职员,对甲、乙两位候选人进行了面试和笔试,面试中包括形体和口才,笔试中包括专业水平和创新能力考察,他们的成绩(百分制)如下表:
候选人 | 面试 | 笔试 | ||
形体 | 口才 | 专业水平 | 创新能力 | |
甲 | 86 | 90 | 96 | 92 |
乙 | 92 | 88 | 95 | 93 |
若公司根据经营性质和岗位要求认为:形体、口才、专业水平、创新能力按照5:5:4:6的比确定,请计算甲、乙两人各自的平均成绩,看看谁将被录取?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y=kx的图象经过点(3,-6).
(1)求这个函数的解析式;
(2)画出这个函数图象;
(3)判断点A(4,-2)、点B(-1.5,3)是否在这个函数图象上;
(4)图象上有两点C(x1,y1),D(x2,y2),如果x1>x2,比较y1,y2的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com