
ЁОЬтФПЁПдкЁїABCжаЃЌBC=ACЃЌЁЯC=90ЁуЃЌжБНЧЖЅЕуCдкxжсЩЯЃЌвЛШёНЧЖЅЕуBдкyжсЩЯЃЎ
ЃЈ1ЃЉШчЭМЂйШєADгкДЙжБxжсЃЌДЙзуЮЊЕуDЃЎЕуCзјБъЪЧЃЈЉ1ЃЌ0ЃЉЃЌЕуAЕФзјБъЪЧЃЈЉ3ЃЌ1ЃЉЃЌЧѓЕуBЕФзјБъЃЎ
ЃЈ2ЃЉШчЭМЂкЃЌжБНЧБпBCдкСНзјБъжсЩЯЛЌЖЏЃЌШєyжсЧЁКУЦНЗжЁЯABCЃЌACгыyжсНЛгкЕуDЃЌЙ§ЕуAзїAEЁЭyжсгкEЃЌЧыВТЯыBDгыAEгадѕбљЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФВТЯыЃЎ
ЃЈ3ЃЉШчЭМЂлЃЌжБНЧБпBCдкСНзјБъжсЩЯЛЌЖЏЃЌЪЙЕуAдкЕкЫФЯѓЯоФкЃЌЙ§AЕузїAFЁЭyжсгкFЃЌдкЛЌЖЏЕФЙ§ГЬжаЃЌЧыВТЯыOCЃЌAFЃЌOBжЎМфгадѕбљЕФЙиЯЕЃЈжБНгаДГіНсТлЃЌВЛашвЊжЄУїЃЉ

ЁОД№АИЁПЃЈ1ЃЉЃЈ0ЃЌ2ЃЉЃЛЃЈ2ЃЉBD=2AFЃЛЃЈ3ЃЉOC=OB+AF.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉжЛвЊЧѓГіRtЁїADCЁеRtЁїCOBМДПЩЧѓЃЎ
ЃЈ2ЃЉЯШЫЕУїBDгыAEгадѕбљЕФЪ§СПЙиЯЕЃЌШЛКѓеыЖдЕУЕНЕФЪ§СПЙиЯЕЃЌзїГіКЯЪЪЕФИЈжњЯпЃЌЛГіЯргІЕФЭМаЮЃЌИљОнЕШбќШ§НЧаЮЕзБпЩЯЕФИпЁЂЕзБпЩЯЕФжаЯпЁЂЖЅНЧЕФЦНЗжЯпШ§ЯпКЯвЛЃЌПЩвдзюжежЄЕУЫљвЊЫЕУїЕФЪ§СПЙиЯЕЃЛ
ЃЈ3ЃЉЯШВТЯыOCЁЂAFЁЂOBжЎМфЕФЙиЯЕЃЌШЛКѓИљОнВТЯызїГіКЯЪЪЕФИЈжњЯпЃЌЛГіЯргІЕФЭМаЮЃЌШЛКѓжЄУїЫљвЊжЄУїЕФНсТлМДПЩЃЎ
ЪдЬтНтЮіЃК(1)ЁпЕуCзјБъЪЧ(1,0),ЕуAЕФзјБъЪЧ(3,1)
ЁрAD=OCЃЌ
дкRtЁїADCКЭRtЁїCOBжаЃЌ ![]() ЃЌ
ЃЌ
ЁрRtЁїADCЁеRtЁїCOB(HL)ЃЌ
ЁрOB=CD=2ЃЌ
ЁрЕуBЕФзјБъЪЧ(0ЃЌ2)ЃЛ
(2)BD=2AFЃЌ
РэгЩЃКзїAEЕФбгГЄЯпНЛBCЕФбгГЄЯпгкЕуFЃЌШчЯТЭМЫљЪОЃЌ

ЁпЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌBC=ACЃЌжБНЧЖЅЕуCдкxжсЩЯЃЌAEЁЭyжсгкEЃЌ
ЁрЁЯBCA=ЁЯACF=90ЁуЃЌЁЯAED=90ЁуЃЌ
ЁрЁЯDBC+ЁЯBDC=90ЁуЃЌЁЯDAE+ЁЯADE=90ЁуЃЌ
ЁпЁЯBDC=ЁЯADEЃЌ
ЁрЁЯDBC=ЁЯFACЃЌ
дкЁїBDCКЭЁїAFCжаЃЌ
 ЃЌ
ЃЌ
ЁрЁїBDCЁеЁїAFC(ASA)
ЁрBD=AFЃЌ
ЁпBEЁЭAEЃЌyжсЧЁКУЦНЗжЁЯABCЃЌ
ЁрAF=2AEЃЌ
ЁрBD=2AFЃЛ
(3)OC=OB+AFЃЌ
жЄУїЃКзїAEЁЭOCгкЕуEЃЌШчЯТЭМЫљЪОЃЌ

ЁпAEЁЭOCЃЌAFЁЭyжсЃЌ
ЁрЫФБпаЮOFAEЪЧОиаЮЃЌЁЯAEC=90ЁуЃЌ
ЁрAF=OEЃЌ
ЁпЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌBC=ACЃЌжБНЧЖЅЕуCдкxжсЩЯЃЌЁЯBOC=90ЁуЃЌ
ЁрЁЯBCA=90ЁуЃЌ
ЁрЁЯBCO+ЁЯCBO=90ЁуЃЌЁЯBCO+ЁЯACE=90ЁуЃЌ
ЁрЁЯCBO=ЁЯACEЃЌ
дкЁїBOCКЭЁїCEOжаЃЌ
 ЃЌ
ЃЌ
ЁрЁїBOCЁеЁїCEO(AAS)
ЁрOB=CEЃЌ
ЁпOC=OE+ECЃЌOE=AFЃЌOB=ECЃЌ
ЁрOC=OB+AF.


 дЦФЯЪІДѓИНаЁвЛЯпУћЪІЬсгХзївЕЯЕСаД№АИ
дЦФЯЪІДѓИНаЁвЛЯпУћЪІЬсгХзївЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЗжБ№вдЕуAКЭЕуBЮЊдВаФЃЌДѓгк![]() ABЕФГЄЮЊАыОЖЛЛЁЃЌСНЛЁЯрНЛгкЕуMЃЌNЃЌзїжБЯпMNЃЌНЛBCгкЕуDЃЌСЌНгADЃЎШєЁїADCЕФжмГЄЮЊ10ЃЌAB=7ЃЌдђЁїABCЕФжмГЄЮЊ ЃЎ
ABЕФГЄЮЊАыОЖЛЛЁЃЌСНЛЁЯрНЛгкЕуMЃЌNЃЌзїжБЯпMNЃЌНЛBCгкЕуDЃЌСЌНгADЃЎШєЁїADCЕФжмГЄЮЊ10ЃЌAB=7ЃЌдђЁїABCЕФжмГЄЮЊ ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈжаДэЮѓЕФгаЃЈЁЁЁЁЃЉ
ЂйОјЖджЕЪЧЫќБОЩэЕФЪ§гаСНИіЃЌЫќУЧЪЧ0КЭ1
ЂквЛИіЪ§ЕФОјЖджЕБиЮЊе§Ъ§
Ђл2ЕФЯрЗДЪ§ЕФОјЖджЕЪЧ2
ЂмШЮКЮЪ§ЕФОјЖджЕЖМВЛЪЧИКЪ§
A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
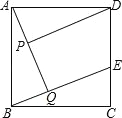
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдке§ЗНаЮABCDжаЃЌЕуEдкБпCDЩЯЃЌAQЁЭBEгкЕуQЃЌDPЁЭAQгкЕуPЃЎ
ЃЈ1ЃЉЧѓжЄЃКAP=BQЃЛ
ЃЈ2ЃЉдкВЛЬэМгШЮКЮИЈжњЯпЕФЧщПіЯТЃЌЧыжБНгаДГіЭМжаЫФЖдЯпЖЮЃЌЪЙУПЖджаНЯГЄЯпЖЮгыНЯЖЬЯпЖЮГЄЖШЕФВюЕШгкPQЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪ§жсЩЯБэЪОећЪ§ЕФЕуГЦЮЊећЕуЃЌФГЪ§жсЕФЕЅЮЛГЄЖШЪЧ1РхУзЃЌШєдкетИіЪ§жсЩЯЫцвтЛГівЛЬѕГЄ2018РхУзЕФЯпЖЮABЃЌдђЯпЖЮABИЧзЁЕФећЕуИіЪ§гаЃЈЁЁЁЁЃЉ
A. 2018Лђ2019 B. 2017Лђ2018 C. 2016Лђ2017 D. 2019Лђ2020
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгУЗДжЄЗЈжЄУї:ШчЙћСНИіећЪ§ЕФЛ§ЪЧХМЪ§ФЧУДетСНИіећЪ§жажСЩйгавЛИіЪЧХМЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁїABCжаЃЌШєЁЯC-ЁЯB=ЁЯAЃЌдђЁїABCЕФЭтНЧжазюаЁЕФНЧЪЧ______ЃЈЬюЁАШёНЧЁБЁЂЁАжБНЧЁБЛђЁАЖлНЧЁБЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫљЪіЭМаЮжаЃЌЪЧжсЖдГЦЭМаЮгжЪЧжааФЖдГЦЭМаЮЕФЪЧ ЃЈ ЃЉ
A.ЦНааЫФБпаЮB.ЕШБпШ§НЧаЮC.е§ЮхБпаЮD.СтаЮ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com