
有红、黄、蓝三种颜色的旗帜各三面,在每种颜色的旗帜上分别标有号码1、2、3,现任意抽取3面,它们的颜色与号码均不相同的概率是_________.
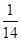
解析试题分析:抽取3面旗,总共的情况计算思路为:第一面旗有9种,第二面有(9-1)即8种,第三面有(9-1-1)即7种,则总的情况有9乘以8乘以7等于504种;
要求颜色和号码都不同的情况计算思路为:第一面旗还是有9种情况;
第二面旗的情况为:除去第一面已选的颜色外,还剩另外2种颜色本来是6种情况,但是第一面旗肯定能确定一个号码,所以剩下的2种颜色中与第一面旗选的号码必须不一样,则选了第一面旗后,第二面旗的选择就只有4种情况了; 而第一面旗和第二面旗选定后,第三面旗就已经确定唯一了,即轮到第三面旗的时候就没的选了,前面2面旗已经把颜色和号码都定死了.
根据乘法公式可知:
任意抽取3面旗,一共有9×8×7=504种情况,
三面旗颜色与号码都不一样的情况一共有9×4×1=36种情况
∴它们的颜色与号码均不相同的概率是
考点:利用乘法公式求概率
点评:解题的关键是求得总共的情况数与要求颜色和号码都不同的情况数.


科目:初中数学 来源: 题型:阅读理解
 (体验探究题)阅读下列解题过程并填空.
(体验探究题)阅读下列解题过程并填空.| m1 |
| n |
| m2 |
| n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com