
| A. | 矩形 | B. | 菱形 | C. | 等腰梯形 | D. | 正方形 |
分析 连接对角线,利用三角形中位线性质得:EF是△ABD的中位线,则EF=$\frac{1}{2}$BD;同理得GH=$\frac{1}{2}$BD,EH=$\frac{1}{2}$AC,GF=$\frac{1}{2}$AC,根据矩形对角线相等得:EF=GH=EH=GF,则中点四边形EFGH是菱形.
解答 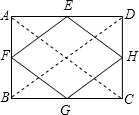 解:矩形ABCD中,E、F、G、H分别是AD、AB、BC、CD的中点,
解:矩形ABCD中,E、F、G、H分别是AD、AB、BC、CD的中点,
连接 AC、BD,
则EF=$\frac{1}{2}$BD,GH=$\frac{1}{2}$BD,EH=$\frac{1}{2}$AC,GF=$\frac{1}{2}$AC,
又∵AC=BD,
∴EF=GH=EH=GF,
∴四边形EFGH是菱形,
∴顺次连接矩形四边中点得到的四边形一定是菱形;
故选B.
点评 本题考查了中点四边形,连对角线构建三角形,运用三角形中位线的性质:三角形的中位线平行于第三边,且等于第三边的一半;以矩形对角线相等为中间量得出结论.


科目:初中数学 来源: 题型:选择题
| A. | AB∥CD,AD∥BC | B. | AB=CD,AD∥BC | C. | AB∥CD,AB=CD | D. | ∠A=∠C,∠B=∠D |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,D为AB的中点,CE=3BE,CF=2AF,四边形CEDF的面积为17,则△ABC的面积为( )
如图,在△ABC中,D为AB的中点,CE=3BE,CF=2AF,四边形CEDF的面积为17,则△ABC的面积为( )| A. | 22 | B. | 23 | C. | 24 | D. | 25 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,为测量池塘岸边A、B两点之间的距离,小亮在池塘的一侧选取一点O,测得OA、OB的中点D、E之间的距离是14米,则A、B两点之间的距离是( )
如图,为测量池塘岸边A、B两点之间的距离,小亮在池塘的一侧选取一点O,测得OA、OB的中点D、E之间的距离是14米,则A、B两点之间的距离是( )| A. | 18 米 | B. | 24米 | C. | 28米 | D. | 30米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
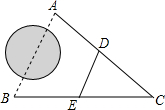 如图,A、B两地被建筑物阻隔,为测量A、B两地间的距离,在地面上选一点C,连接CA、CB,分别取CA、CB的中点D、E,若测得DE的长为36m,那么A、B两地间的距离是( )
如图,A、B两地被建筑物阻隔,为测量A、B两地间的距离,在地面上选一点C,连接CA、CB,分别取CA、CB的中点D、E,若测得DE的长为36m,那么A、B两地间的距离是( )| A. | 60m | B. | 65m | C. | 70m | D. | 72m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5}$+$\sqrt{2}$=$\sqrt{7}$ | B. | $\sqrt{{a^2}-{b^2}}$=a-b | C. | $\frac{\sqrt{6}+\sqrt{8}}{2}$=$\sqrt{3}$+$\sqrt{4}$=$\sqrt{3}$+2 | D. | a$\sqrt{x}$-b$\sqrt{x}$=(a-b)$\sqrt{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y=y2 | C. | y1<y2 | D. | 不能比较 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com