
【题目】某工厂设计了一款成本为20元件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价x(元件) | … | 30 | 40 | 50 | 60 | … |
每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
(1)研究发现,每天销售量y与单价x满足一次函数关系,求出y与x的关系式;
(2)当地物价部门规定,该工艺品销售单价最高不能超过50元件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润8000元?
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】已知tan∠MON=2,矩形ABCD的边AB在射线OM上,AD=2,AB=m,CF⊥ON,垂足为点F.
(1)如图(1),作AE⊥ON,垂足为点E. 当m=2时,求线段EF的长度;
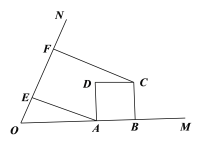
图(1)
(2)如图(2),联结OC,当m=2,且CD平分∠FCO时,求∠COF的正弦值;
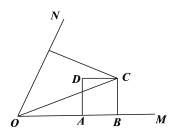
图(2)
(3)如图(3),当△AFD与△CDF相似时,求m的值.
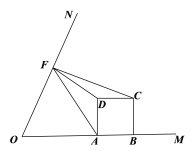
图(3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:把一个半圆与抛物线的一部分组成的封闭图形称为“蛋圆”.
如图,抛物线y=x2﹣2x﹣3与x轴交于点A,B,与y轴交于点D,以AB为直径,在x轴上方作半圆交y轴于点C,半圆的圆心记为M,此时这个半圆与这条抛物线x轴下方部分组成的图形就称为“蛋圆”.
(1)直接写出点A,B,C的坐标及“蛋圆”弦CD的长;
A ,B ,C ,CD= ;
(2)如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.
①求经过点C的“蛋圆”切线的解析式;
②求经过点D的“蛋圆”切线的解析式;
(3)由(2)求得过点D的“蛋圆”切线与x轴交点记为E,点F是“蛋圆”上一动点,试问是否存在S△CDE=S△CDF,若存在请求出点F的坐标;若不存在,请说明理由;
(4)点P是“蛋圆”外一点,且满足∠BPC=60°,当BP最大时,请直接写出点P的坐标.
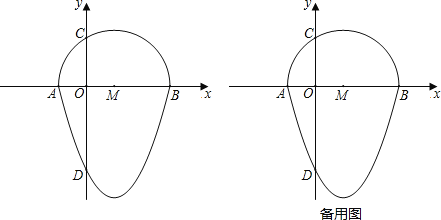
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租汽车公司计划购买A型和B型两种节能汽车,若购买A型汽车4辆,B型汽车7辆,共需310万元;若购买A型汽车10辆,B型汽车15辆,共需700万元.
(1)A型和B型汽车每辆的价格分别是多少万元?
(2)该公司计划购买A型和B型两种汽车共10辆,费用不超过285万元,且A型汽车的数量少于B型汽车的数量,请你给出费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为![]() 万元/辆,经销一段时间后发现:当该型号汽车售价定为
万元/辆,经销一段时间后发现:当该型号汽车售价定为![]() 万元/辆时,平均每周售出
万元/辆时,平均每周售出![]() 辆;售价每降低
辆;售价每降低![]() 万元,平均每周多售出
万元,平均每周多售出![]() 辆.
辆.
(1)当售价为![]() 万元/辆时,平均每周的销售利润为___________万元;
万元/辆时,平均每周的销售利润为___________万元;
(2)若该店计划平均每周的销售利润是![]() 万元,为了尽快减少库存,求每辆汽车的售价.
万元,为了尽快减少库存,求每辆汽车的售价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,B,C,E是同一直线上的三个点, 四边形ABCD与四边形CEFG都是正方形.连接BG,DE.
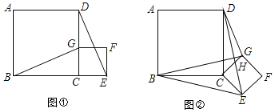
(1)探究BG与DE之间的数量关系, 并证明你的结论;
(2)当正方形CEFG绕点C在平面内顺时针转动到如图②所示的位置时,线段BG和ED有何关系? 写出结论并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第一象限
的图象交于第一象限![]() ,
,![]() 两点,与坐标轴交于
两点,与坐标轴交于![]() 、
、![]() 两点,连结
两点,连结![]() ,
,![]() .
.
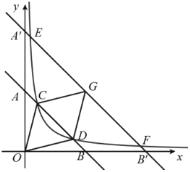
(1)求![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)将直线![]() 向上平移
向上平移![]() 个单位到直线
个单位到直线![]() ,此时,直线
,此时,直线![]() 上恰有一点
上恰有一点![]() 满足
满足![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把函数C1:y=ax2﹣2ax﹣3a(a≠0)的图象绕点P(m,0)旋转180°,得到新函数C2的图象,我们称C2是C1关于点P的相关函数.C2的图象的对称轴与x轴交点坐标为(t,0).
(1)填空:t的值为 (用含m的代数式表示)
(2)若a=﹣1,当![]() ≤x≤t时,函数C1的最大值为y1,最小值为y2,且y1﹣y2=1,求C2的解析式;
≤x≤t时,函数C1的最大值为y1,最小值为y2,且y1﹣y2=1,求C2的解析式;
(3)当m=0时,C2的图象与x轴相交于A,B两点(点A在点B的右侧).与y轴相交于点D.把线段AD原点O逆时针旋转90°,得到它的对应线段A′D′,若线A′D′与C2的图象有公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com