
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据平行线的性质,三角形的三边关系,三角形的高、中线的概念,以及平移的性质进行判断即可.
解答 解:①两条直线被第三条直线所截,则同旁内角不一定互补,故①错误;
②若线段a、b、c,满足b+c>a,则以a、b、c为边不一定能组成三角形,故②错误;
③三角形的三条高可能在三角形内部,故③错误;
④三角形的一条中线把该三角形分成面积相等的两部分,故④正确;
⑤△ABC在平移过程中,对应线段一定平行(或在一条直线上)且相等,故⑤错误.
故选:A.
点评 本题主要考查了三角形的高线、中线,三角形的三边关系以及平移的性质的运用,解题时注意:在运用三角形三边关系判定三条线段能否构成三角形时,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.锐角三角形的三条高相交于三角形内一点,直角三角形有两条高与直角边重合,另一条高在三角形内部,它们的交点是直角顶点;钝角三角形三条高所在直线相交于三角形外一点.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:选择题
| A. | 若|x|=|y|,则x=y | B. | 若x2=y2,则x=y | C. | 若$\sqrt{x^2}=|y|$,则x=y | D. | 若$\root{3}{x}=\root{3}{y}$,则x=y |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
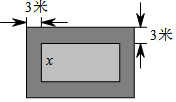 一标志性建筑的底面呈长方形,长是宽的2倍,在其四周铺上花岗岩,形成一个边宽为3米的长方形框(如图所示).已知铺这个框恰好用了504块边长为0.5米的正方向花岗岩(接缝忽略不计).若设此标志性建筑底面长方形的宽为x米,给出下列方程:
一标志性建筑的底面呈长方形,长是宽的2倍,在其四周铺上花岗岩,形成一个边宽为3米的长方形框(如图所示).已知铺这个框恰好用了504块边长为0.5米的正方向花岗岩(接缝忽略不计).若设此标志性建筑底面长方形的宽为x米,给出下列方程:| A. | ② | B. | ③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
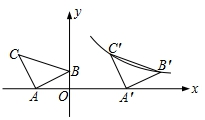 如图,在平面直角坐标系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(-2,0),B(0,1).
如图,在平面直角坐标系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(-2,0),B(0,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com