
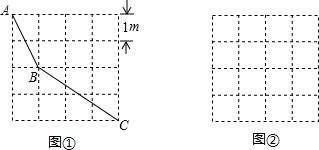
| 5 |
| 13 |
| 5 |
| 13 |
| 10 |
| 10 |
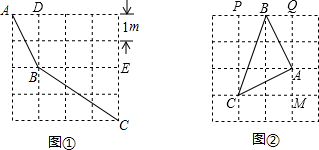
| AD2+DB2 |
| 5 |
| BE2+CE2 |
| 13 |
| 5 |
| 13 |
| PB2+PC2 |
| 10 |
| AQ2+BQ2 |
| 5 |
| AM2+CM2 |
| 5 |
| 5 |
| 13 |


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省江阴市顾山九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作(以下结果保留根号):

(1)利用网格确定该圆弧所在圆的圆心D点的位置,并写出D点的坐标为???????????? ;
(2)连接AD、CD,则⊙D的半径为???????? ,∠ADC的度数为???????? ;
(3)若扇形DAC是一个圆锥的侧面展开图,求该圆锥底面半径.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 的一个等腰△ABC,三角形的顶点必须在格点上.
的一个等腰△ABC,三角形的顶点必须在格点上.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com