
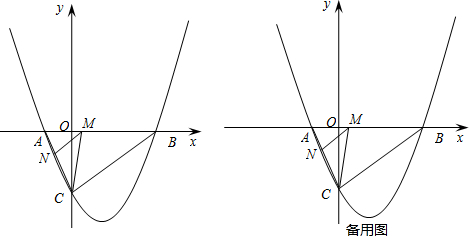
分析 (1)根据一元二次方程解法得出A,B两点的坐标,再利用交点式求出二次函数解析式;
(2)首先判定△MNA∽△BCA.得出$\frac{NH}{CO}$=$\frac{AM}{AB}$,进而得出函数的最值;
(3)分别根据当AF为平行四边形的边时,AF平行且等于DE与当AF为平行四边形的对角线时,分析得出符合要求的答案.
解答 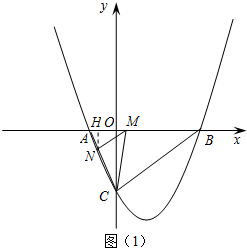 解:(1)∵x2-4x-12=0,
解:(1)∵x2-4x-12=0,
∴x1=-2,x2=6.
∴A(-2,0),B(6,0),
又∵抛物线过点A、B、C,故设抛物线的解析式为y=a(x+2)(x-6),
将点C的坐标代入,求得a=$\frac{1}{3}$,
∴抛物线的解析式为y=$\frac{1}{3}$x2-$\frac{4}{3}$x-4;
(2)设点M的坐标为(m,0),过点N作NH⊥x轴于点H(如图(1)).
∵点A的坐标为(-2,0),点B的坐标为(6,0),
∴AB=8,AM=m+2,
∵MN∥BC,
∴△MNA∽△BCA.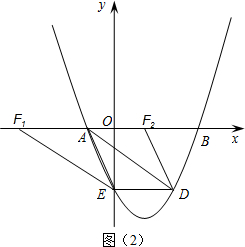
∴$\frac{NH}{CO}$=$\frac{AM}{AB}$,
∴$\frac{NH}{4}$=$\frac{m+2}{8}$,
∴NH=$\frac{m+2}{2}$,
∴S△CMN=S△ACM-S△AMN=$\frac{1}{2}$•AM•CO-$\frac{1}{2}$AM•NH,
=$\frac{1}{2}$(m+2)(4-$\frac{m+2}{2}$)=-$\frac{1}{4}$m2+m+3,
=-$\frac{1}{4}$(m-2)2+4.
∴当m=2时,S△CMN有最大值4.
此时,点M的坐标为(2,0);
(3)∵点D(4,k)在抛物线y=$\frac{1}{3}$x2-$\frac{4}{3}$x-4上,
∴当x=4时,k=-4,
∴点D的坐标是(4,-4).
①如图(2),当AF为平行四边形的边时,AF平行且等于DE,
∵D(4,-4),
∴DE=4.
∴F1(-6,0),F2(2,0),
②如图(3),当AF为平行四边形的对角线时,设F(n,0),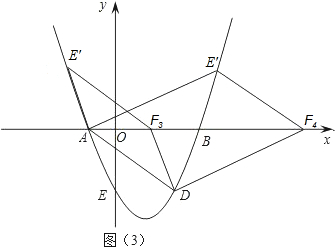
∵点A的坐标为(-2,0),
则平行四边形的对称中心的横坐标为:$\frac{n+(-2)}{2}$,
∴平行四边形的对称中心坐标为($\frac{n-2}{2}$,0),
∵D(4,-4),
∴E'的横坐标为:$\frac{n-2}{2}$-4+$\frac{n-2}{2}$=n-6,
E'的纵坐标为:4,
∴E'的坐标为(n-6,4).
把E'(n-6,4)代入y=$\frac{1}{3}$x2-$\frac{4}{3}$x-4,得n2-16n+36=0.
解得n=8±2$\sqrt{7}$.F3(8-2$\sqrt{7}$,0),F4(8+2$\sqrt{7}$,0),
综上所述F1(-6,0),F2(2,0),F3(8-2$\sqrt{7}$,0),F4(8+2$\sqrt{7}$,0).
点评 此题主要考查了二次函数的综合应用,二次函数的综合应用是初中阶段的重点题型,特别注意利用数形结合是这部分考查的重点,也是难点,同学们应重点掌握.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
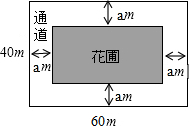 如图,为美化环境,某小区计划在一块长为60m,宽为40m的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建同样宽的通道,当通道的面积与花圃的面积之比等于3:5时,求此时通道的宽.
如图,为美化环境,某小区计划在一块长为60m,宽为40m的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建同样宽的通道,当通道的面积与花圃的面积之比等于3:5时,求此时通道的宽.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
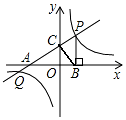 如图,直线y=$\frac{1}{2}$x+3分别交x轴、y轴于点A、C,交双曲线y=$\frac{k}{x}$在第一象限内于点P,过点P作PB⊥x轴于点B,若S△ABC=12.
如图,直线y=$\frac{1}{2}$x+3分别交x轴、y轴于点A、C,交双曲线y=$\frac{k}{x}$在第一象限内于点P,过点P作PB⊥x轴于点B,若S△ABC=12.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com