
如图,在坐标系xOy中,已知D(﹣5,4),B(﹣3,0),过D点分别作DA、DC垂直于x轴,y轴,垂足分别为A、C两点,动点P从O点出发,沿x轴以每秒1个单位长度的速度向右运动,运动时间为t秒.

(1)当t为何值时,PC∥DB;
(2)当t为何值时,PC⊥BC;
(3)以点P为圆心,PO的长为半径的⊙P随点P的运动而变化,当⊙P与△BCD的边(或边所在的直线)相切时,求t的值.
解:(1)∵D(﹣5,4),B(﹣3,0),过D点分别作DA、DC垂直于x轴,y轴,垂足分别为A、C两点,
∴DC=5,OC=4,OB=3,
∵DC⊥y轴,x轴⊥y轴,∴DC∥BP。
∵PC∥DC,∴四边形DBPC是平行四边形。
∴DC=BP=5。∴OP=5﹣3=2。
∵2÷1=2,∴当t为2秒时,PC∥BD。
(2)∵PC⊥BC,x轴⊥y轴,∴∠COP=∠COB=∠BCP=90。
∴∠PCO+∠BCO=90°,∠CPO+∠PCO=90°。∴∠CPO=∠BCO。
∴△PCO∽△CBO。∴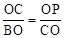 ,即
,即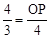 ,解得
,解得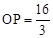 。
。
∵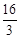 ÷1=
÷1=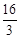 ,∴当t为
,∴当t为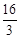 秒时,PC⊥BC。
秒时,PC⊥BC。
(3)设⊙P的半径是R,分为三种情况:
①当⊙P与直线DC相切时,
如图1,过P作PM⊥DC交DC延长线于M,
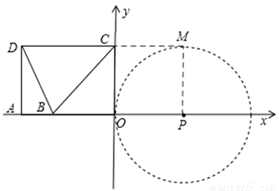
则PM=OC=4=OP,
∵4÷1=4,∴t=4秒。
②如图2,当⊙P与BC相切时,
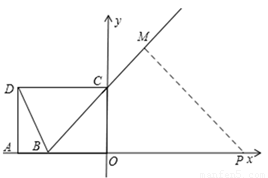
∵∠BOC=90°,BO=3,OC=4,∴由勾股定理得:BC=5。
∵∠PMB=∠COB=90°,∠CBO=∠PBM,∴△COB∽△PBM。
∴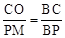 ,即
,即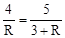 ,解得R=12。
,解得R=12。
∵12÷1=12,∴t=12秒。
③如图3,当⊙P与DB相切时,
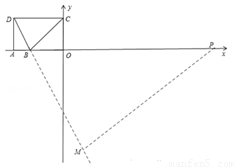
根据勾股定理得: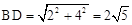 ,
,
∵∠PMB=∠DAB=90°,∠ABD=∠PBM
∴△ADB∽△MPB。
∴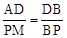 ,即
,即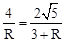 ,解得
,解得 。
。
∵(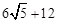 )÷1=
)÷1=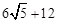 ,∴t
,∴t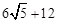 秒。
秒。
综上所述,当⊙P与△BCD的边(或边所在的直线)相切时,t=4秒或12秒或t=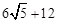 秒。
秒。
【解析】(1)过D点分别作DA、DC垂直于x轴,y轴,垂足分别为A、C两点,求出DC=5,OC=4,OB=3,根据四边形DBPC是平行四边形求出DC=BP=5,求出OP=2即可。
(2)证△PCO∽△CBO,得出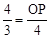 ,求出
,求出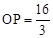 即可。
即可。
(3)设⊙P的半径是R,分为①当⊙P与直线DC相切时,②当⊙P与BC相切时,③当⊙P与DB相切时三种情况讨论即可。


科目:初中数学 来源: 题型:
 (2013•湘潭)如图,在坐标系xOy中,已知D(-5,4),B(-3,0),过D点分别作DA、DC垂直于x轴,y轴,垂足分别为A、C两点,动点P从O点出发,沿x轴以每秒1个单位长度的速度向右运动,运动时间为t秒.
(2013•湘潭)如图,在坐标系xOy中,已知D(-5,4),B(-3,0),过D点分别作DA、DC垂直于x轴,y轴,垂足分别为A、C两点,动点P从O点出发,沿x轴以每秒1个单位长度的速度向右运动,运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 x2+bx-2的图象过C点.
x2+bx-2的图象过C点.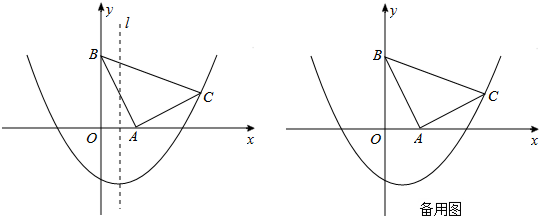
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(湖南湘潭卷)数学(解析版) 题型:解答题
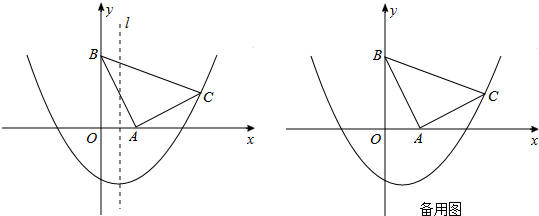
如图,在坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线 的图象过C点.
的图象过C点.

(1)求抛物线的解析式;
(2)平移该抛物线的对称轴所在直线l.当l移动到何处时,恰好将△ABC的面积分为相等的两部分?
(3)点P是抛物线上一动点,是否存在点P,使四边形PACB为平行四边形?若存在,求出P点坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:2013年湖南省湘潭市中考数学试卷(解析版) 题型:解答题
 x2+bx-2的图象过C点.
x2+bx-2的图象过C点.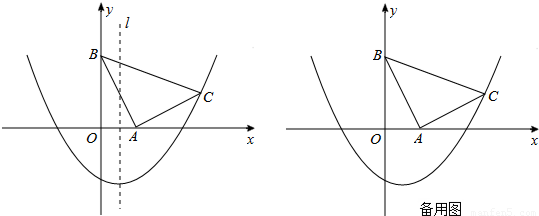
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com