
����Ŀ��ij�̳����۵�ij����Ʒÿ���ı����![]() Ԫ��������۵İ������ۣ��Կ�ӯ��
Ԫ��������۵İ������ۣ��Կ�ӯ��![]() ����ʱ������Ʒÿ���ڿ�����
����ʱ������Ʒÿ���ڿ�����![]() �����г����鷢�֣��ڰ������۵Ļ����ϣ�������Ʒÿ����
�����г����鷢�֣��ڰ������۵Ļ����ϣ�������Ʒÿ����![]() Ԫ��ÿ���ڿɶ���
Ԫ��ÿ���ڿɶ���![]() ������ÿ����Ʒ����
������ÿ����Ʒ����![]() Ԫ��
Ԫ��![]() Ϊ��������ÿ���ڵ�����Ϊ
Ϊ��������ÿ���ڵ�����Ϊ![]() Ԫ
Ԫ
��1���������Ʒÿ���Ľ���Ϊ����Ԫ��
��2�����ۼ�Ϊ����ʱ��ÿ���ڵ����������������Ƕ��٣�
��3��2019��2�¸�����Ʒÿ���ڵ��ۼ۾�Ϊÿ��![]() Ԫ����2019��2�µ�������
Ԫ����2019��2�µ�������![]() Ԫ�������
Ԫ�������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡���1��40����2���ۼ�Ϊ![]() ��
��![]() Ԫʱ��ÿ�����������Ϊ
Ԫʱ��ÿ�����������Ϊ![]() Ԫ����3��
Ԫ����3��![]()
��������
��1����ɱ�Ϊ![]() Ԫ����������ã�80��80%
Ԫ����������ã�80��80%![]() =
=![]() �����ɽ��
�����ɽ��
��2����������õ�![]() �����ö��κ��������ʣ����ɽ��
�����ö��κ��������ʣ����ɽ��
��3������ÿ���ڵ�����ǡΪ24000��4=6000Ԫ����һԪ���η��̣�������̵Ľ⣬��һ��ȷ��ȡֵ��Χ��
�⣺��1�������Ϊ![]() Ԫ����
Ԫ����![]() ��
��
��ã�![]()
���������Ʒÿ���Ľ���Ϊ40Ԫ��
��2����ÿ���ڵ�����Ϊ![]() ����
����
![]() ��
��
��![]() ��������
��������![]() ��
��![]() ʱ��
ʱ��![]() �����ֵΪ
�����ֵΪ![]() Ԫ��
Ԫ��
���ۼ�Ϊ![]() ��
��![]() Ԫʱ��ÿ�����������Ϊ
Ԫʱ��ÿ�����������Ϊ![]() Ԫ��
Ԫ��
��3��������ã�![]() ��
��
��ã�![]() ��
��![]() ��
��
��![]() ��Ԫ����
��Ԫ����![]() ��Ԫ����
��Ԫ����
��2019��2�¸�����Ʒÿ���ڵ��ۼ۾�Ϊÿ��![]() Ԫ��
Ԫ��
��![]() ��
��


 ����С��ʿ���������ϵ�д�
����С��ʿ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ƶ��������Ŀ��ٷ�չ�����ڻ������Ĺ�������Ӧ�˶�����Ϊ�˽�ijС������ʹ�ù��������������ij�о�С������ɷø�С����10λ���õ���10λ����һ����ʹ�ù��������Ĵ����ֱ�Ϊ��17��12��15��20��17��0��7��26��17��9��
��1���������ݵ���λ������ ������������ ����
��2��������10λ����һ����ʹ�ù���������ƽ��������
��3������С����200�������Թ��Ƹ�С������һ����ʹ�ù����������ܴ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
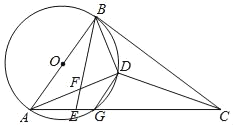
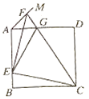
����Ŀ����ͼ��AB����O��ֱ����AC����O��G��E��AG��һ�㣬DΪ��BCE���ģ�BE��AD��F���ҡ�DBE����BAD��
(1)��֤��BC����O�����ߣ�
(2)��֤��DF��DG��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
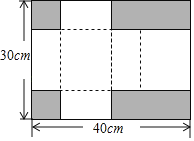
����Ŀ����ͼ����һ�ų�����ֽ����ĸ����Ϸֱ����2��С�����κ�2��С�����Σ���Ӱ���ּ������IJ��֣���ʣ��IJ��ֿ����۳�һ���иǵij�������ӣ�ֽ��ĺ�Ⱥ��Բ��ƣ�����������ֽ��߳��ֱ�Ϊ40cm��30cm�����۳ɵij�������ӱ������950cm2����ʱ��������ӵ����Ϊ_____cm3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
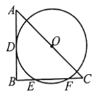
����Ŀ����ͼ������![]() ����
����![]() Ϊб��
Ϊб��![]() �ϣ���
�ϣ���![]() ��
��![]() �����ڵ�
�����ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() ����֪
����֪![]() ��
��![]() ����
����![]() �ij����� ��
�ij����� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊa����E�ڱ�AB���˶��������A��B�غϣ�����DAM=45������F������AM�ϣ���![]() ��CF��AD�ཻ�ڵ�G������EC��EF��EG�������н��ۣ��١�ECF=45������
��CF��AD�ཻ�ڵ�G������EC��EF��EG�������н��ۣ��١�ECF=45������![]() ���ܳ�Ϊ
���ܳ�Ϊ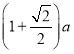 ����
����![]() ����
����![]() ����������ֵ
����������ֵ![]() .������ȷ�Ľ�����____.����д������ȷ���۵���ţ�
.������ȷ�Ľ�����____.����д������ȷ���۵���ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y��ax2+bx+c��a��0����ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C����OC��2OB�����н��ۣ���abc��0����a+b+c��0����ac��2b+4��0����OAOB��![]() ��������ȷ�Ľ����У�������
��������ȷ�Ľ����У�������
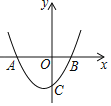
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
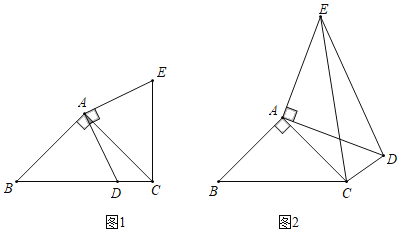
����Ŀ����ͼ1���ڡ�ABC�У���BAC��90����AB��AC��DΪBC����һ��(�����B��C�غ�)�����߶�AD�Ƶ�A��ʱ����ת90���õ�AE������EC.
(1)��ͼ1��ͨ��ͼ����ת�����ʿ�֪AD��_____����DAE��_____��.
��������⣩
(2)��ͼ1��֤��BC��DC+EC��
����չ���죩
��ͼ2���ڡ�ABC�У���BAC��90����AB��AC��DΪ��ABC��һ�㣬�ҡ�ADC��45�����Խ��߶�AD�Ƶ�A��ʱ����ת90���õ�AE������EC��ED.
(3)��AD��6��CD��3����BD�ij�.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com