
【题目】如图,在平面直角坐标系中,![]() 的直角项点
的直角项点![]() 在
在![]() 轴的正半轴上,顶点
轴的正半轴上,顶点![]() 的纵坐标为
的纵坐标为![]() ,
,![]() ,
,![]() .点
.点![]() 是斜边
是斜边![]() 上的一个动点,则
上的一个动点,则![]() 的周长的最小值为___________.
的周长的最小值为___________.

【答案】![]() +2
+2![]()
【解析】
由题意AB=3,则![]() 中,AB=
中,AB=![]() OB,可得∠AOB=30°,根据勾股定理求出OA,作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,则此时PA+PC的值最小,求出AM,求出AD,求出DN、CN,根据勾股定理求出CD,即可得出答案.
OB,可得∠AOB=30°,根据勾股定理求出OA,作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,则此时PA+PC的值最小,求出AM,求出AD,求出DN、CN,根据勾股定理求出CD,即可得出答案.
解:作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,则此时PA+PC的值最小,
∵A、D关于OB对称,
∴OB垂直平分AD,
∴DP=PA,
∴PA+PC=PD+PC=CD,
∵顶点B的纵坐标为3, ![]() ,
,
∴AB=3,OA=![]() =3
=3![]() ,∠BOA=30°,∠B=60°,
,∠BOA=30°,∠B=60°,
由三角形面积公式得:![]() ×OA×AB=
×OA×AB=![]() ×OB×AM,
×OB×AM,
即:![]() ×3
×3![]() ×3=
×3=![]() ×6×AM
×6×AM
解得:AM=![]() ,
,
∴AD=2×![]() =3
=3![]() ,
,
∵∠AMB=90°,∠B=60°,
∴∠BAM=30°,
∵∠BAO=90°,
∴∠OAM=60°,
∵DN⊥OA,
∴DN∥AB,
∴∠NDA=∠BAM=30°,
∴AN=![]() AD=
AD=![]() ,
,
由勾股定理得:DN=![]() =
=![]() ,
,
∵OC=![]() AC,
AC,
∴OC=![]() ,AC=2
,AC=2![]() ,
,
∴CN=AC-AN=2![]() -
-![]() =
=![]() ,
,
在Rt△DNC中,由勾股定理得:DC=![]() =
= =
=![]() ,
,
即PA+PC的最小值是![]() ,
,
∴△PAC周长的最小值为:![]() +2
+2![]() .
.
故答案为:![]() +2
+2![]() .
.


科目:初中数学 来源: 题型:
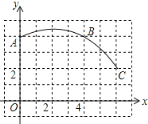
【题目】如图,一段圆弧与长度为1的正方形网格的交点是A、B、C.
(1)请完成以下操作:
①以点O为原点,垂直和水平方向为轴,网格边长为单位长,建立平面直角坐标系;
②根据图形提供的信息,标出该圆弧所在圆的圆心D,并连接AD、CD;
(2)请在(1)的基础上,完成下列填空:⊙D的半径为__________;点(6,–2)在⊙D__________;(填“上”、“内”、“外”)∠ADC的度数为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
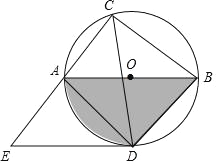
【题目】如图,⊙O的直径AB=12,弦AC=6,∠ACB的平分线交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD.
(1)由AB,BD,![]() 围成的阴影部分的面积是 ;
围成的阴影部分的面积是 ;
(2)求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
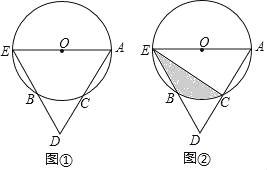
【题目】如图①,AE是⊙O的直径,点C是⊙O上的点,连结AC并延长AC至点D,使CD=CA,连结ED交⊙O于点B.
(1)求证:点C是劣弧![]() 的中点;
的中点;
(2)如图②,连结EC,若AE=2AC=6,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
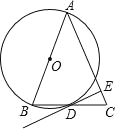
【题目】如图,在等腰△ABC中,AB=AC,以AB为直径作⊙O交底边BC于D.
(1)求证:BD=CD;
(2)若AB=3,cos∠ABC=![]() ,在腰AC上取一点E使AE=
,在腰AC上取一点E使AE=![]() ,试判断DE与⊙O的位置关系,并证明.
,试判断DE与⊙O的位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,D是半圆O上的三等分点,直径AB=4,连接AD,AC,作DE⊥AB,垂足为E,DE交AC于点F.
(1)求证:AF=DF.
(2)求阴影部分的面积(结果保留π和根号)
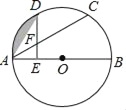
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 以上均不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年暑假,都有许多驴友为实现自己的一个梦想,骑自行车丈量中国最美的公路川藏线。![]() 、
、![]() 两个驴友团队于同一天出发前往目的地拉萨。
两个驴友团队于同一天出发前往目的地拉萨。![]() 队走317国道,结果30天到达。
队走317国道,结果30天到达。![]() 队走318国道,总路程比
队走318国道,总路程比![]() 队少200千米,且路况更好,平均每天比
队少200千米,且路况更好,平均每天比![]() 队多骑行20千米,结果
队多骑行20千米,结果![]() 队比
队比![]() 队提前8天到达拉萨.
队提前8天到达拉萨.
(1)求318国道全程为多少千米?
(2)骑行过程中,![]() 队每人每天平均花费150元。
队每人每天平均花费150元。![]() 队开始有3个人同行,计划每人每天花费110元,后来又有几个人加入队伍,实际每增加1人时,每人每天的平均花费就减少5元。若最终
队开始有3个人同行,计划每人每天花费110元,后来又有几个人加入队伍,实际每增加1人时,每人每天的平均花费就减少5元。若最终![]() 、
、![]() 两队骑行的人数相同(均不超过10人),两队共花费了36900元,求两驴友团队各有多少人?
两队骑行的人数相同(均不超过10人),两队共花费了36900元,求两驴友团队各有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com