
分析 过C作CG⊥AB于G,根据已知条件设BC=2,AB=3,由勾股定理得AC=$\sqrt{5}$,由射影定理得CB2=BG•AB,得到BG=$\frac{4}{3}$,由旋转的性质得CE=BC=2,FC═AC=$\sqrt{5}$,∠F=∠A,根据勾股定理得到EG=$\sqrt{C{E}^{2}-C{G}^{2}}$=$\sqrt{{2}^{2}-(\frac{4}{3})^{2}}$=$\frac{2\sqrt{5}}{3}$,根据根于是矩形的性质得到BE=$\frac{4\sqrt{5}}{4}$,根据相似三角形的性质即可得到结论.
解答 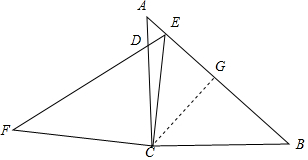 解:过C作CG⊥AB于G,
解:过C作CG⊥AB于G,
∵cosB=$\frac{2}{3}$,
设BC=2,AB=3,由勾股定理得AC=$\sqrt{5}$,
由射影定理得CB2=BG•AB,
∴BG=$\frac{4}{3}$,
由旋转的性质得CE=BC=2,FC═AC=$\sqrt{5}$,
∠F=∠A,
∴EG=$\sqrt{C{E}^{2}-C{G}^{2}}$=$\sqrt{{2}^{2}-(\frac{4}{3})^{2}}$=$\frac{2\sqrt{5}}{3}$,BG=EG,
∴BE=$\frac{4\sqrt{5}}{4}$,
∴AE=3-$\frac{4\sqrt{5}}{3}$,$\frac{AE}{EB}$=$\frac{3-\frac{4\sqrt{5}}{3}}{\frac{4\sqrt{5}}{3}}$=$\frac{9\sqrt{5}-20}{4}$,
∵∠FDC=∠ADE,
∴△ADF∽△FDC,
∴$\frac{AD}{FD}$=$\frac{AE}{CF}$=$\frac{3-\frac{4\sqrt{5}}{3}}{\sqrt{5}}$=$\frac{9\sqrt{5}-20}{3}$,
故答案为:$\frac{9\sqrt{5}-20}{4}$,$\frac{9\sqrt{5}-20}{3}$.
点评 该题主要考查了旋转变换的性质、勾股定理、相似三角形的判定等几何知识点及其应用问题;解题的方法是作辅助线,将分散的条件集中;解题的关键是灵活运用旋转变换的性质、勾股定理等几何知识点来分析、判断、推理或解答.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 比赛场次 | 胜场 | 负场 | 积分 |
| m | 0 | m | m |
| 8 | 3 | 5 | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com