
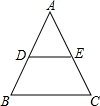
 如图,在△ABC中,AB=AC,DE∥BC,则下列结论中不正确的是( )
如图,在△ABC中,AB=AC,DE∥BC,则下列结论中不正确的是( )| A. | AD=AE | B. | DB=EC | C. | ∠ADE=∠C | D. | DE=$\frac{1}{2}$BC |
分析 由DE与BC平行,得到三角形ADE与三角形ABC相似,由相似得比例,根据AB=AC,得到AD=AE,进而确定出DB=EC,再由两直线平行同位角相等,以及等腰三角形的底角相等,等量代换得到∠ADE=∠C,而DE不一定为中位线,即DE不一定为BC的一半,即可得到正确选项.
解答 解:∵DE∥BC,
∴$\frac{AD}{AB}$=$\frac{AE}{AC}$,∠ADE=∠B,
∵AB=AC,
∴AD=AE,DB=EC,∠B=∠C,
∴∠ADE=∠C,
而DE不一定等于$\frac{1}{2}$BC,
故选D.
点评 此题考查了等腰三角形的判定与性质,以及平行线的性质,熟练掌握等腰三角形的判定与性质是解本题的关键.


科目:初中数学 来源: 题型:选择题
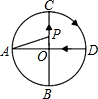 如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y关于点P运动的时间x(单位:秒)的函数图象大致是( )
如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y关于点P运动的时间x(单位:秒)的函数图象大致是( )| A. | 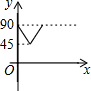 | B. | 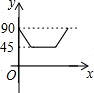 | C. | 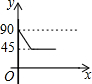 | D. | 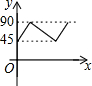 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
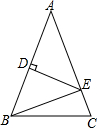 如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB=16cm.
如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB=16cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
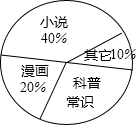 为了解学生课外阅读的喜好,某校从八年级1200名学生中随机抽取50名学生进行问卷调查,整理数据后绘制如图所示的统计图.由此可估计该年级喜爱“科普常识”的学生约有360人.
为了解学生课外阅读的喜好,某校从八年级1200名学生中随机抽取50名学生进行问卷调查,整理数据后绘制如图所示的统计图.由此可估计该年级喜爱“科普常识”的学生约有360人.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≤3 | B. | x≠4 | C. | x≥3且x≠4 | D. | x≤3或x≠4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
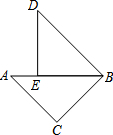 如图,△ABC和△DBE都是等腰直角三角形,点E在AB上,若△ABC经旋转后能与△DBE重合,则旋转中心为( )
如图,△ABC和△DBE都是等腰直角三角形,点E在AB上,若△ABC经旋转后能与△DBE重合,则旋转中心为( )| A. | 点A | B. | 点B | C. | 点C | D. | 点E |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
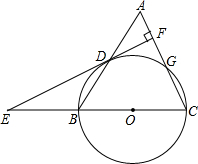 如图,已知等腰△ABC,AC=BC=10.AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
如图,已知等腰△ABC,AC=BC=10.AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com