
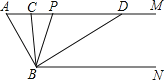
【题目】综合与探究:如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与点A不重合).BC,BD别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠ABN、∠CBD的度数;根据下列求解过程填空.
解:∵AM∥BN,
∴∠ABN+∠A=180°
∵∠A=60°,
∴∠ABN= ,
∴∠ABP+∠PBN=120°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP、∠PBN= ,( )
∴2∠CBP+2∠DBP=120°,
∴∠CBD=∠CBP+∠DBP= .
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,直接写出∠ABC的度数.
【答案】(1)120°,2∠PBD,角平分线的定义,60°(2)∠APB=2∠ADB.不随点P运动变化,见解析;(3)30°
【解析】
(1)由AM∥BN,∠A=60°可得∠ABP+∠PBN=120°,再根据角平分线的定义知∠ABP=2∠CBP、∠PBN=2∠DBP,可得2∠CBP+2∠DBP=120°,即∠CBD=∠CBP+∠DBP=60°;
(2)由AM∥BN得∠APB=∠PBN、∠ADB=∠DBN,根据BD平分∠PBN知∠PBN=2∠DBN,从而可得∠APB=2∠ADB;
(3)由AM∥BN得∠ACB=∠CBN,当∠ACB=∠ABD时有∠CBN=∠ABD,得∠ABC+∠CBD=∠CBD+∠DBN,即∠ABC=∠DBN,根据∠ABN=120°,∠CBD=60°可得答案.
解:

(1)∵AM∥BN,
∴∠ABN+∠A=180°,
∵∠A=60°,
∴∠ABN=120°
∴∠ABP+∠PBN=120°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP、∠PBN=2∠PBD,(角平分线的定义),
∴2∠CBP+2∠DBP=120°,
∴∠CBD=∠CBP+∠DBP=60°.
故答案为120°,2∠PBD,角平分线的定义,60°.
(2)∠APB与∠ADB之间数量关系是:∠APB=2∠ADB.不随点P运动变化.
理由是:∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN(两直线平行内错角相等),
∵BD平分∠PBN(已知),
∴∠PBN=2∠DBN(角平分线的定义),
∴∠APB=∠PBN═2∠DBN=2∠ADB(等量代换),
即∠APB=2∠ADB.
(3)结论:∠ABC=30°.
理由:∵AM∥BN,∴∠ACB=∠CBN,
当∠ACB=∠ABD时,则有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN,
由(1)可知∠ABN=120°,∠CBD=60°,
∴∠ABC+∠DBN=60°,
∴∠ABC=30°


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2![]() 2x+c的顶点A在直线l:y=x
2x+c的顶点A在直线l:y=x![]() 5上.
5上.
(1)求抛物线顶点A的坐标;
(2)设抛物线与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状;
(3)在直线l上是否存在一点P,使以点P、A、B、D为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料阅读:对于一个圆和一个正方形给出如下定义:若圆上存在到此正方形四条边距离都相等的点,则称这个圆是该正方形的“等距圆”.
如图1,在平面直角坐标系xOy中,正方形ABCD的顶点A的坐标为(2,4),顶点C、D在x轴上,且点C在点D的左侧.
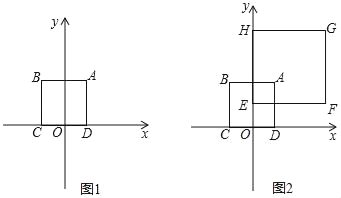
(1)当r=2![]() 时,在P1(2,0),P2(﹣4,2),P3(2
时,在P1(2,0),P2(﹣4,2),P3(2![]() ,2),P4(2﹣2
,2),P4(2﹣2![]() ,0)中可以成为正方形ABCD的“等距圆”的圆心的是 ;
,0)中可以成为正方形ABCD的“等距圆”的圆心的是 ;
(2)若点P坐标为(﹣2,﹣1),则当⊙P的半径r= 时,⊙P是正方形ABCD的“等距圆”.试判断此时⊙P与直线BD的位置关系?并说明理由.
(3)如图2,在正方形ABCD所在平面直角坐标系xOy中,正方形EFGH的顶点F的坐标为(8,2),顶点E、H在y轴上,且点H在点E的上方.若⊙P同时为上述两个正方形的“等距圆”,且与BC所在直线相切,求⊙P的圆心P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
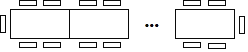
【题目】一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图所示的方式进行拼接.
(1)若把4张这样的餐桌拼接起来,四周可坐 人;
(2)若把n张这样的餐桌拼接起来,四周可坐 人;
(3)若把9张这样的餐桌拼接起来,四周可坐 人;
(4)若用餐的人数有50人,则这样的餐桌需要多少张?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每逢金秋送爽之时,正是大闸蟹上市的旺季,也是吃蟹的最好时机,可谓膏肥黄美.


某经销商购进一批雌蟹、雄蟹共1000只,进价均为每只40元,然后以雌蟹每只75元、雄蟹每只60元的价格售完,共获利29000元.
(1)求该经销商分别购进雌蟹、雄蟹各多少只?
(2)民间有“九雌十雄”的说法,即九月吃雌蟹,十月吃雄蟹.十月份,在进价不变的情况下该经销商决定调整价格,将雌蟹的价格在九月份的基础上下调![]() (降价后售价不低于进价),雄蟹的价格上涨
(降价后售价不低于进价),雄蟹的价格上涨![]() ,同时雌蟹的销量较九月下降了
,同时雌蟹的销量较九月下降了![]() ,雄蟹的销量上升了
,雄蟹的销量上升了![]() ,结果十月份的销售额比九月份增加了1000元,求a的值.
,结果十月份的销售额比九月份增加了1000元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米。

(1)这个梯子的顶端离地面有多高?
(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点(﹣1,y1),(2,y2),![]() 在反比例函数y=﹣
在反比例函数y=﹣![]() 的图象上,则下列关系式正确的是( )
的图象上,则下列关系式正确的是( )
A.y3<y2<y1B.y2<y3<y1
C.y3<y1<y2D.y2<y1<y3
查看答案和解析>>
科目:初中数学 来源: 题型:
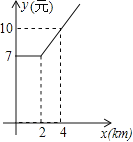
【题目】某地出租车计费方法如图,x(km)表示行驶里程,y(元)表示车费,请根据图象解答下列问题:
(1)该地出租车的起步价是 元;
(2)当x>2时,求y与x之间的函数关系式;
(3)若某乘客有一次乘出租车的里程为18km,则这位乘客需付出租车车费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com