
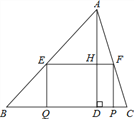
����Ŀ����ͼ������ABC�У���B��45�㣬BC��5����AD��4������EFPQ��һ��QP��BC���ϣ�E��F�ֱ���AB��AC�ϣ�AD��EF�ڵ�H��
��1��������EFPQΪ������ʱ���������εı߳���
��2����EF��x����xΪ��ֵʱ������EFPQ�������������������
��3��������EFPQ��������ʱ���þ���EFPQ��ÿ��1����λ���ٶ�������BC���������˶��������εĶ���Q����C��ʱֹͣ�˶��������˶�ʱ��Ϊt�룬����EFPQ����ABC�ص����ֵ����ΪS����S��t�ĺ�����ϵʽ����д��t��ȡֵ��Χ��
���𰸡���1��������EFPQΪ������ʱ���߳�Ϊ![]() ����2����x=
����2����x=![]() ʱ������EFPQ��������������Ϊ5����3����0��t��
ʱ������EFPQ��������������Ϊ5����3����0��t��![]() ʱ��S =5-2t2����
ʱ��S =5-2t2����![]() ��t��2.5ʱ��S��
��t��2.5ʱ��S��![]() -2t����2.5��t��3ʱ��S��2t2-12t+18
-2t����2.5��t��3ʱ��S��2t2-12t+18
����������1���������ɵ�![]() ����
����![]() �����㼴��.
�����㼴��.
��2��������![]() ��x��ʾ��EH����ʾ������EFPQ����������ö��κ�������������ֵ��
��x��ʾ��EH����ʾ������EFPQ����������ö��κ�������������ֵ��
��3����0��t��![]() ��
��![]() ��2.5��t��3��������������ۼ���.
��2.5��t��3��������������ۼ���.
(1)���ı���EFPQΪ���Σ�
��EF��BC��
![]() ��
��
��![]() ��
��
���![]()
�൱����EFPQΪ������ʱ���߳�Ϊ![]() .
.
����xΪ![]() ʱ������EFPQΪ�����Σ�
ʱ������EFPQΪ�����Σ�
��2���ߡ�B=45�㣬
��![]() ��
��
��![]()
��EF��BC��
���AEH�ס�ABD����![]() ��
��
��EF��BC�����AFH�ס�ACD����![]() ��
��
��![]() ����
����![]() ����
����![]() ��
��
��֪EF=x����EH=![]() ��
��
�ߡ�B=45�㣬
��![]() =4��
=4��![]() ��
��
S����EFPQ![]()
�൱x=![]() ʱ������EFPQ��������������Ϊ5��
ʱ������EFPQ��������������Ϊ5��
��3����ͼ�٣���0��t��![]() ʱ
ʱ

��EF��AC��M�㣬FP��AC��N�㣬
�ߡ�MNF�ס�CAD��
��![]() ��
��
��![]() ��
��
��FN=4t ��
��S=5-![]() t��4t��
t��4t��
=5-2t2
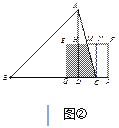
��ͼ�ڣ���![]() ʱ
ʱ
��EF��AC��M�㣬��C��CN��EF��N�㣬
�ߡ�CNM�ס�ADC
��![]() ��
��
��![]() ��
��
��MN=![]() ��
��
��FN=t-![]() ��
��
��S=5-![]() ��t-
��t-![]() +t����
+t����
=![]() -2t ��
-2t ��
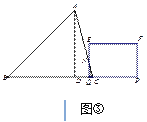
��ͼ�ۣ���2.5��t��3ʱ
��EQ��AC��N�㣬
�ߡ�CQN�ס�CDA
��![]() ��
��
![]() ��
��
��NQ=12-4t��
��S=![]() (3-t)(12-4t)
(3-t)(12-4t)
=2t2-12t+18


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ԭ��Ϊ0����A��B��C�������ϵ����㣬��B��Ӧ����λ1��AB=6��BC=2������P��Qͬʱ��A��C�������ֱ���ÿ��2�����ȵ�λ��ÿ��1�����ȵ�λ���ٶ��������������˶������˶�ʱ��Ϊt�루t��0��
��1�����A��C�ֱ��Ӧ������
��2������t������P��Q�ֱ��Ӧ�������ú�t��ʽ�ӱ�ʾ��
��3�����ʵ�tΪ��ֵʱ��OP=OQ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �У�
��![]() ��
��![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ����ͼ�еĵ����������У� ��
����ͼ�еĵ����������У� ��
A.2��B.3��C.4��D.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��ֱ��ABΪ2cm����BCΪ1cm����ACB��ƽ�������O���ڵ�D����AB���ڵ�E��PΪAB�ӳ�����һ�㣬����PC����PC��PE��
��1����AC��AD�ij���
��2�����ж�ֱ��PC���O��λ�ù�ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ���ϵ�һ�㣬
���ϵ�һ�㣬![]() ��
��![]() ���е㣬����
���е㣬����![]() ��
��![]() ��ƽ���߽�
��ƽ���߽�![]() ���ӳ�����
���ӳ�����![]() ����
����![]() ������
������![]() ��
��
��1����֤��![]() ��
��![]() ���е㣻
���е㣻
��2�����![]() ���Բ²��ı���
���Բ²��ı���![]() ����״����֤����Ľ��ۣ�
����״����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
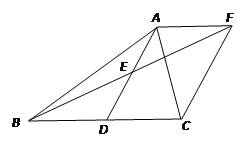
����Ŀ���ڡ�ABC�У���BAC=45�㣬��BD=2��CD=3��AD��BC��D������ABD��AB���ڵ�ֱ���۵���ʹ��D���ڵ�E��������ACD��AC���ڵ�ֱ���۵���ʹ��D���ڵ�F�����ֱ��ӳ�EB��FCʹ�佻�ڵ�M��
(1)�ж��ı���AEMF����״��������֤����
(2)��AD=x�����ù��ɶ�������������x�ķ���ģ�ͣ����ı���AEMF�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
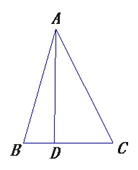
����Ŀ����֪�߶�![]() ���߶�
���߶�![]() ��
��

��1����Ҫ����ͼ(������Χ�ۼ�����д����)��
�ӳ��߶�![]() ����
����![]() ��ʹ
��ʹ![]() �������ӳ��߶�
�������ӳ��߶�![]() ����
����![]() ��ʹ
��ʹ![]() ��
��
��2�����![]() ��
��![]() �ֱ����߶�
�ֱ����߶�![]() ��
��![]() ���е㣬��
���е㣬��![]() ��
��![]() �����߶�
�����߶�![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ����
����![]() ����
����![]() ��һ��ֱ�ߣ�
��һ��ֱ�ߣ�![]() ��
��![]() �ֱ���ֱ��
�ֱ���ֱ��![]() �����㣬��
�����㣬��![]() ��
��
��1����ֱ��![]() ����
����![]() ���ڲ�����
���ڲ�����![]() ������
������![]() �ϣ����������������⣺
�ϣ����������������⣺
����ͼ1����![]() ��
��![]() ��
��
��![]()
![]() ��
��![]()
![]() ������
������![]() ������
������![]() ������
������![]() ������
������
����ͼ2����![]() ��������һ������
��������һ������![]() ��
��![]() ��ϵ������ ��ʹ���е�����������Ȼ��������֤���������۳�����
��ϵ������ ��ʹ���е�����������Ȼ��������֤���������۳�����
��2����ͼ3����ֱ��![]() ����
����![]() ���ⲿ��
���ⲿ��![]() �������
�������![]() �����߶�������ϵ�ĺ������루��Ҫ��֤������
�����߶�������ϵ�ĺ������루��Ҫ��֤������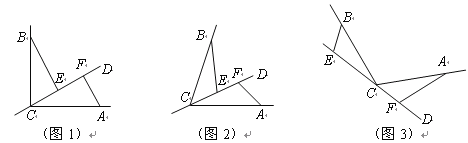
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com