
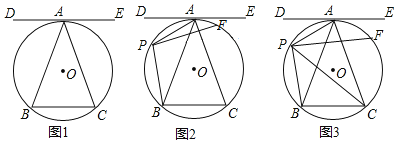
【题目】.如图,⊙O是△ABC的外接圆,直线DE是⊙O的切线,点A为切点,DE∥BC;
(1)如图1.求证:AB=AC;
(2)如图2.点P是弧AB上一动点,连接PA、PB,作PF⊥PB,垂足为点P,PF交⊙O于点F, 求证:∠BAC=2∠APF;
(3)如图3.在(2)的条件下,连接PC,PA=![]() ,PB=
,PB=![]() ,PC=
,PC=![]() ,求线段PF的长.
,求线段PF的长.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)如图1中,连接OA,延长AO交BC于H,只需证明AH垂直平分BC即可;(2)如图2中,连接OA、BF,首先证明BF是直径,可得∠1=∠3,再证明OA平方∠BAC即可解决问题;(3)如图3中,连接AF、CF、BF、OA延长OA交BC于H,在AB上取一点K,使得∠BPK=∠APC,作BM⊥PC于M,利用△APC∽△KPB和△APK∽△CPB推出![]() ,设BC=
,设BC=![]() k,AB=AC=
k,AB=AC=![]() k,⊙O的半径为r,在Rt△ABH中,AH=
k,⊙O的半径为r,在Rt△ABH中,AH=![]() k,在Rt△OBH中,OB2=OH2+BH2,得到r2=(
k,在Rt△OBH中,OB2=OH2+BH2,得到r2=(![]() k)2+(
k)2+(![]() k-r)2,推出r=
k-r)2,推出r=![]() k,在Rt△FBC中,sin∠BFC=
k,在Rt△FBC中,sin∠BFC=![]() ,推出cos∠BFC=
,推出cos∠BFC=![]() ,在Rt△PBM中,PB=5
,在Rt△PBM中,PB=5![]() ,由∠BPC=∠BFC,推出PM=PBcos∠PBC=
,由∠BPC=∠BFC,推出PM=PBcos∠PBC=![]() ×5
×5![]() =4
=4![]() ,BM=PBsin∠BPC=5
,BM=PBsin∠BPC=5![]() ×
×![]() =3
=3![]() ,CM=PC=PM=3
,CM=PC=PM=3![]() ,
,
推出BM=CM=3![]() ,则BC=
,则BC=![]() CM=6,可得
CM=6,可得![]() k=6,求得k=3
k=6,求得k=3![]() ,求出半径即可解决问题.
,求出半径即可解决问题.
(1)证明:如图1中,连接OA,延长AO交BC于H.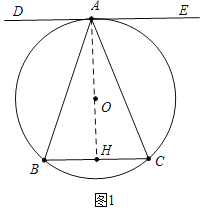
∵DE是切线,
∴OA⊥DE,
∵DE∥BC,
∴AH⊥BC,
∴BH=CH,
∴AB=AC.
(2)证明:如图2中,连接OA、BF.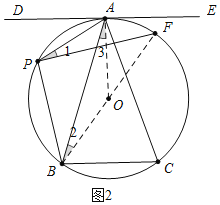
∵BP⊥PF,
∴∠BPF=90°,
∴BF是直径,
∵OB=OA,
∴∠2=∠3,
∵∠1=∠2,
∴∠1=∠3,
由(1)可知,AB=AC,AO⊥BC,
∴OA平分∠BAC,
∴∠BAC=2∠3=2∠1,
∴∠BAC=2∠APF.
(3)解:如图3中,连接AF、CF、BF、OA延长OA交BC于H,在AB上取一点K,使得∠BPK=∠APC,作BM⊥PC于M.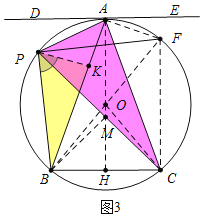
∵∠BPK=∠APC,∠AFP=∠PBK,
∴△APC∽△KPB,
∴PBAC=BKPC ①
∵∠APK=∠CPB,∠PAK=∠PCB,
∴△APK∽△CPB,
∴PABC=PCAK ②,
①+②得PBAC+PABC=PCAB,
∵AB=AC,
∴![]() ,
,
设BC=![]() k,AB=AC=
k,AB=AC=![]() k,⊙O的半径为r.
k,⊙O的半径为r.
在Rt△ABH中,AH=![]() =
=![]() k,
k,
在Rt△OBH中,∵OB2=OH2+BH2,
∴r2=(![]() k)2+(
k)2+(![]() k-r)2,
k-r)2,
∴r=![]() k,
k,
在Rt△FBC中,sin∠BFC=![]() ,
,
∴cos∠BFC=
在Rt△PBM中,∵PB=5![]() ,∠BPC=∠BFC,
,∠BPC=∠BFC,
∴PM=PBcos∠PBC=![]() ×5
×5![]() =4
=4![]() ,BM=PBsin∠BPC=5
,BM=PBsin∠BPC=5![]() ×
×![]() =3
=3![]() ,
,
∴CM=PC=PM=3![]() ,
,
∴BM=CM=3![]() ,
,
∴BC=![]() CM=6,
CM=6,
∴![]() k=6,
k=6,
∴k=3![]() ,
,
∴r=![]() ×3
×3![]() =5,
=5,
在Rt△PBF中,PF=![]() =5
=5![]() .
.


科目:初中数学 来源: 题型:
【题目】在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G,连接EG、CG,如图(1),易证 EG=CG且EG⊥CG.
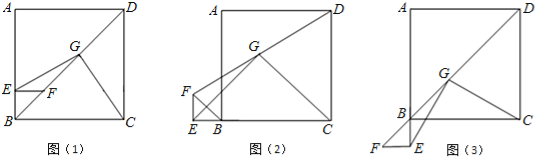
(1)将△BEF绕点B逆时针旋转90°,如图(2),则线段EG和CG有怎样的数量关系和位置关系?请直接写出你的猜想.
(2)将△BEF绕点B逆时针旋转180°,如图(3),则线段EG和CG又有怎样的数量关系和位置关系?请写出你的猜想,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
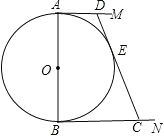
【题目】如图,⊙O的直径是AB=12cm,AM、BN是它的两条切线,DE与⊙O相切于点E,并与AM、BN分别相交于D、C两点,设AD=x,BC=y,则y与x的函数解析式为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有3张正面分别写有数字![]() ,0,1的卡片,它们的背面完全相同,现将这3张卡片背面朝上洗匀,小明先从中任意抽出一张卡片记下数字为x;小亮再从剩下的卡片中任意取出一张记下数字为y,记作
,0,1的卡片,它们的背面完全相同,现将这3张卡片背面朝上洗匀,小明先从中任意抽出一张卡片记下数字为x;小亮再从剩下的卡片中任意取出一张记下数字为y,记作![]() .
.
![]() 用列表或画树状图的方法列出所有可能的点P的坐标;
用列表或画树状图的方法列出所有可能的点P的坐标;
![]() 若规定:点
若规定:点![]() 在第二象限小明获胜;点
在第二象限小明获胜;点![]() 在第四象限小亮获胜,游戏规则公平吗?
在第四象限小亮获胜,游戏规则公平吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是 ( )
A. “打开电视机,正在播放《新闻联播》”是必然事件
B. 天气预报“明天降水概率 50%”,是指明天有一半的时间会下雨
C. 数据 6,6,7,7,8 的中位数与众数均为 7
D. 甲、乙两人在相同的条件下各射击 10 次,他们成绩的平均数相同,方差分别是 S 甲=0.3,S 乙=0.4,则甲的成绩 更稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 xOy 中,已知正比例函数 y1=﹣2x 的图象与反比例函数 y2=![]() 的图象交于 A(﹣1,a),B 两点.
的图象交于 A(﹣1,a),B 两点.
(1)求出反比例函数的解析式及点 B 的坐标;
(2)观察图象,请直接写出满足 y≤2 的取值范围;
(3)点 P 是第四象限内反比例函数的图象上一点,若△POB 的面积为 1,请直接写出点 P的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示.在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,连接CP.下列结论:①∠ACB=2∠APB;②S△PAC:S△PAB=AC:AB;③BP垂直平分CE;④∠PCF=∠CPF.其中,正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com