
分析 (1)设彩色地砖采购x块,则购买单色地砖(100-x)块,根据彩色地砖和单色地砖的总价为5600建立一元一次方程求出其解即可;
(2)设购进彩色地砖y块,则单色地砖购进(60-y)块,根据采购地砖的费用不超过3300元建立不等式,求出其解即可.
解答 解:(1)设购买彩色地砖x块,则购买单色地砖(100-x)块,根据题意,可得:
80x+40(100-x)=5600
解得:x=40,100-x=60
经检验,符合题意
答:购买彩色地砖40块,单色地砖60块.
(2)设彩色地砖购买y块,根据题意可得:
80y+40(60-y)≤3300
解得y≤22.5.
因为y为正整数,
所以y的最大值为22,
答:彩色地砖最多购买22块.
点评 本题考查了列一元一次方程解实际问题的运用,列一元一次不等式解实际问题的运用,解答时认真分析单价×数量=总价的关系建立方程及不等式是关键.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限内交于点P(a,b),则a与b的数量关系是a+b=0.
如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限内交于点P(a,b),则a与b的数量关系是a+b=0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某公司计划用32m长的材料沿墙建造的长方形仓库,仓库的一边靠墙,已知墙长16m,设长方形的宽AB为xm.
如图,某公司计划用32m长的材料沿墙建造的长方形仓库,仓库的一边靠墙,已知墙长16m,设长方形的宽AB为xm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
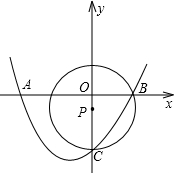 如图,抛物线y=ax2+bx+c(a≠0)经过x轴上的两点A(x1,0)、B(x2,0)和y轴上的点C(0,8),⊙P的圆心P在y轴上,且经过B、C两点,若b=2a,AB=6.
如图,抛物线y=ax2+bx+c(a≠0)经过x轴上的两点A(x1,0)、B(x2,0)和y轴上的点C(0,8),⊙P的圆心P在y轴上,且经过B、C两点,若b=2a,AB=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com