
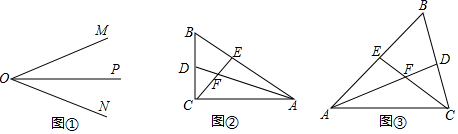
分析 (1)在∠MON的两边上以O为端点截取相等的两条相等的线段,两个端点与角平分线上任意一点相连,所构成的两个三角形全等,即△COB≌△AOB;
(2)根据图(1)的作法,在CG上截取CG=CD,证得△CFG≌△CFD(SAS),得出DF=GF;再根据ASA证明△AFG≌△AFE,得EF=FG,故得出EF=FD;
(3)根据图(1)的作法,在CG上截取AG=AE,证得△EAF≌△GAF(SAS),得出FE=FG;再根据ASA证明△FDC≌△FGC,得DF=FG,故得出EF=FD.
解答 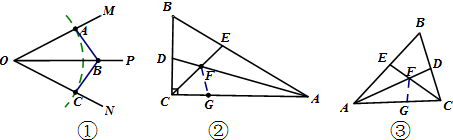 解:(1)如图①所示,△COB≌△AOB,点C即为所求.
解:(1)如图①所示,△COB≌△AOB,点C即为所求.
(2)如图②,在CG上截取CG=CD,
∵CE是∠BCA的平分线,
∴∠DCF=∠GCF,
在△CFG和△CFD中,
$\left\{\begin{array}{l}{CG=CD}\\{∠DCF=∠GCF}\\{CF=CF}\end{array}\right.$,
∴△CFG≌△CFD(SAS),
∴DF=GF.
∵∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,
∴∠FAC=$\frac{1}{2}$∠BAC,∠FCA=$\frac{1}{2}$∠ACB,且∠EAF=∠GAF,
∴∠FAC+∠FCA=$\frac{1}{2}$(∠BAC+∠ACB)=$\frac{1}{2}$(180°-∠B)=60°,
∴∠AFC=120°,
∴∠CFD=60°=∠CFG,
∴∠AFG=60°,
又∵∠AFE=∠CFD=60°,
∴∠AFE=∠AFG,
在△AFG和△AFE中,
$\left\{\begin{array}{l}{∠AFE=∠AFG}\\{AF=AF}\\{∠EAF=∠GAF}\end{array}\right.$,
∴△AFG≌△AFE(ASA),
∴EF=GF,
∴DF=EF;
(3)DF=EF 仍然成立.
证明:如图③,在CG上截取AG=AE,
同(2)可得△EAF≌△GAF(SAS),
∴FE=FG,∠EFA=∠GFA.
又由题可知,∠FAC=$\frac{1}{2}$∠BAC,∠FCA=$\frac{1}{2}$∠ACB,
∴∠FAC+∠FCA=$\frac{1}{2}$(∠BAC+∠ACB)=$\frac{1}{2}$(180°-∠B)=60°,
∴∠AFC=180°-(∠FAC+∠FCA)=120°,
∴∠EFA=∠GFA=180°-120°=60°=∠DFC,
∴∠CFG=∠CFD=60°,
同(2)可得△FDC≌△FGC(ASA),
∴FD=FG,
∴FE=FD.
点评 此题主要考查全等三角形的判定和性质的运用,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造全等三角形.


科目:初中数学 来源: 题型:选择题
| A. | k=1,b=1 | B. | k=0,b=2 | C. | k=-1,b=1 | D. | k=1,b=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
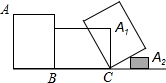 如图,长方形木板的长为4cm,宽为3cm,某同学使之在桌面上做无滑动的翻滚(顺时针方向),木板上点A的位置变化为A→Al→A2,其中第二次翻滚被桌面上的一块小木板挡住,使木板与桌面成30°,则点A滚到A2位置时走过的路径总长为( )
如图,长方形木板的长为4cm,宽为3cm,某同学使之在桌面上做无滑动的翻滚(顺时针方向),木板上点A的位置变化为A→Al→A2,其中第二次翻滚被桌面上的一块小木板挡住,使木板与桌面成30°,则点A滚到A2位置时走过的路径总长为( )| A. | 10cm | B. | 3.5π cm | C. | 4.5π cm | D. | 2.5π cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com