
【题目】如图,将边长为4的正方形ABCD的一边BC与直角边分别是2和4的Rt△GEF的一边GF重合.正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动,当点A和点E重合时正方形停止运动.设正方形的运动时间为t秒,正方形ABCD与Rt△GEF重叠部分面积为S,则S关于t的函数图象为( )
A.
B.
C.
D.
【答案】B
【解析】解:当0≤t≤2时,如图,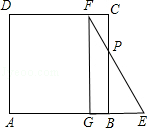
BG=t,BE=2﹣t,
∵PB∥GF,
∴△EBP∽△EGF,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴PB=4﹣2t,
∴S= ![]() (PB+FG)GB=
(PB+FG)GB= ![]() (4﹣2t+4)t=﹣t2+4t;
(4﹣2t+4)t=﹣t2+4t;
当2<t≤4时,S= ![]() FGGE=4;
FGGE=4;
当4<t≤6时,如图,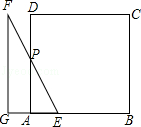
GA=t﹣4,AE=6﹣t,
∵PA∥GF,
∴△EAP∽△EGF,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴PA=2(6﹣t),
∴S= ![]() PAAE=
PAAE= ![]() ×2×(6﹣t)(6﹣t)
×2×(6﹣t)(6﹣t)
=(t﹣6)2 ,
综上所述,当0≤t≤2时,s关于t的函数图象为开口向下的抛物线的一部分;当2<t≤4时,s关于t的函数图象为平行于x轴的一条线段;当4<t≤6时,s关于t的函数图象为开口向上的抛物线的一部分.
故选:B.
分类讨论:当0≤t≤2时,BG=t,BE=2﹣t,运用△EBP∽△EGF的相似比可表示PB=4﹣2t,S为梯形PBGF的面积,则S= ![]() (4﹣2t+4)t=﹣t2+4t,其图象为开口向下的抛物线的一部分;
(4﹣2t+4)t=﹣t2+4t,其图象为开口向下的抛物线的一部分;
当2<t≤4时,S= ![]() FGGE=4,其图象为平行于x轴的一条线段;
FGGE=4,其图象为平行于x轴的一条线段;
当4<t≤6时,GA=t﹣4,AE=6﹣t,运用△EAP∽△EGF的相似比可得到PA=2(6﹣t),所以S为三角形PAE的面积,则S=(t﹣6)2 , 其图象为开口向上的抛物线的一部分.


科目:初中数学 来源: 题型:
【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系为:____________________(直接写出结果).
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP,CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系为:____________________(直接写出结果).
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP,CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】班委会决定,选购圆珠笔、钢笔共22支,送给山区学校的同学。已知圆珠笔每支5元,钢笔每支6元。
(1)若购买圆珠笔、钢笔刚好用去120元,问圆珠笔、钢笔各买了多少支?
(2)若购圆珠笔可9折优惠,钢笔可8折优惠,在所需费用不超过100元的前提下,请你写出一种选购方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列各题:
(1)计算:-22+|5-8|+24÷(-3)×![]() ;
;
(2)化简与计算:
①化简:3x2-[7x-(4x-3)-2x2];
②先化简,再求值:![]() x-2
x-2![]() +
+![]() ,其中x=-2,y=
,其中x=-2,y=![]() ;
;
(3)解方程:
①32x-64=16x+32;
②-![]() =2-
=2-![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】希望中学八年级学生开展踢毽子活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩较好的甲班和乙班5名学生的比赛成绩(单位:个)
1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
经统计发现两班5名学生踢毽子的总个数相等.此时有学生建议,可以通过考查数据中的其它信息作为参考.请你回答下列问题:
(1)求两班比赛数据的中位数;
(2)计算两班比赛数据的方差,并比较哪一个小;
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班?简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空并完成以下证明:
已知:点P在直线CD上,∠BAP+∠APD=180°,∠1=∠2.
求证:AB∥CD,∠E=∠F.
证明:∵∠BAP+∠APD=180°,(已知)
∴AB∥ .( )
∴∠BAP= .( )
又∵∠1=∠2,(已知)
∠3= ﹣∠1,
∠4= ﹣∠2,
∴∠3= (等式的性质)
∴AE∥PF.( )
∴∠E=∠F.( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l:y= ![]() x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1 , 以原点O为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2 , 以原点O为圆心,OB2长为半径画弧交y轴于点A3 , …,按此作法进行下去,则OA2017= .
x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1 , 以原点O为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2 , 以原点O为圆心,OB2长为半径画弧交y轴于点A3 , …,按此作法进行下去,则OA2017= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,直线y=mx与双曲线 ![]() 相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1. 
(1)求m、n的值;
(2)求直线AC的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com