

分析 分别过点A作AM⊥BF于点M,过点C作CN⊥AB于点N,利用勾股定理得出BN的长,再利用相似三角形的判定与性质得出即可.
解答 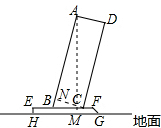 解:过点A作AM⊥BF于点M,过点C作CN⊥AB于点N,如图所示:
解:过点A作AM⊥BF于点M,过点C作CN⊥AB于点N,如图所示:
∵AD=24cm,则NC=24cm,
∴BN=$\sqrt{B{C}^{2}-N{C}^{2}}$=$\sqrt{2{5}^{2}-2{4}^{2}}$=7(cm),
∵∠AMB=∠CNB=90°,∠ABM=∠CBN,
∴△BNC∽△BMA,
∴$\frac{AB}{BF}=\frac{CN}{AM}$,
∴$\frac{75}{25}=\frac{AM}{24}$,
解得:AM=72,
故点A到地面的距离=72+4=76(cm).
故答案为:76.
点评 此题主要考查了勾股定理的应用以及相似三角形的判定与性质,得出△BNC∽△BMA是解题关键.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:解答题
 我们经常利用图形描述问题和分析问题.借助直观的几何图形,把问题变得简明、形象,有助于探索解决问题的思路.
我们经常利用图形描述问题和分析问题.借助直观的几何图形,把问题变得简明、形象,有助于探索解决问题的思路.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 春天来了,小颖要用总长为12米的篱笆围一个长方形花圃,其一边靠墙(墙长9米),另外三边是篱笆,其中BC不超过9米.设垂直于墙的两边AB,CD的长均为x米,长方形花圃的面积为y米2.
春天来了,小颖要用总长为12米的篱笆围一个长方形花圃,其一边靠墙(墙长9米),另外三边是篱笆,其中BC不超过9米.设垂直于墙的两边AB,CD的长均为x米,长方形花圃的面积为y米2.| x(米) | … | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | … |
| y(米2) | … | 13.5 | 16 | 17.5 | 17.5 | 13.5 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠BAC=90°,AB=AC,D、E是BC上的两点,且满足∠DAE=45°.
如图,在△ABC中,∠BAC=90°,AB=AC,D、E是BC上的两点,且满足∠DAE=45°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com