Question

两条平行线被第三条直线所截，一组同旁内角的角平分线

1. A.
   互相垂直
2. B.
   互相平行
3. C.
   相交但不垂直
4. D.
   位置关系不能确定

Answer 1

A
分析：首先根据题意画出图形，由AB∥CD，根据两直线平行，同旁内角互补，即可求得∠BEF+∠DFE=180°，又由EG与FG分别是∠BEF与∠DFE的角平分线，即可求得∠1+∠2=90°，则可得两条平行线被第三条直线所截，一组同旁内角的角平分线互相垂直．
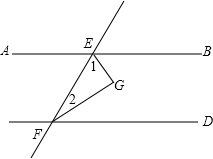
解答：解：∵AB∥CD，
∴∠BEF+∠DFE=180°，
∵EG与FG分别是∠BEF与∠DFE的角平分线，
∴∠1=∠BEF，∠2=∠DFE，
∴∠1+∠2=90°，
∴∠EGF=90°，
∴EG⊥FG．
故选A．
点评：此题考查了平行线的性质与角平分线的定义．此题比较简单，注意两直线平行，同旁内角互补定理的应用，注意数形结合思想的应用．