
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 先将x=2m+n+2和x=m+2n时,多项式x2+4x+6的值相等理解为x=2m+n+2和x=m+2n时,二次函数y=x2+4x+6的值相等,则抛物线的对称轴为直线x=$\frac{3m+3n+2}{2}$,又二次函数y=x2+4x+6的对称轴为直线x=-2,得出$\frac{3m+3n+2}{2}$=-2,化简得m+n=-2,即可求出当x=3(m+n+1)=3(-2+1)=-3时,x2+4x+6的值.
解答 解:∵x=2m+n+2和x=m+2n时,多项式x2+4x+6的值相等,
∴二次函数y=x2+4x+6的对称轴为直线x=$\frac{2m+n+2+m+2n}{2}$=$\frac{3m+3n+2}{2}$,
又∵二次函数y=x2+4x+6的对称轴为直线x=-2,
∴$\frac{3m+3n+2}{2}$=-2,
∴3m+3n+2=-4,m+n=-2,
∴当x=3(m+n+1)=3(-2+1)=-3时,
x2+4x+6=(-3)2+4×(-3)+6=3.
故选:A.
点评 本题考查了二次函数的性质及多项式求值,难度中等.将x=2m+n+2和x=m+2n时,多项式x2+4x+6的值相等理解为x=2m+n+2和x=m+2n时,二次函数y=x2+4x+6的值相等是解题的关键.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
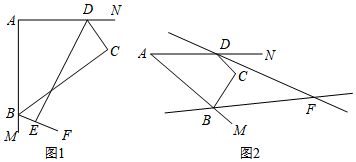
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
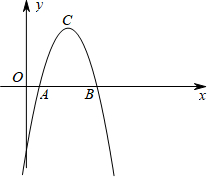 如图,已知与x轴交于点A(1,0)和B(5,0)的抛物线l的顶点为C(3,4),抛物线l′和l关于x轴对称.
如图,已知与x轴交于点A(1,0)和B(5,0)的抛物线l的顶点为C(3,4),抛物线l′和l关于x轴对称.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
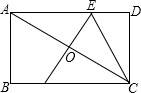 如图,在?ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则△CDE的周长为( )
如图,在?ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则△CDE的周长为( )| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
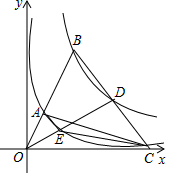 如图,点A为双曲线y=$\frac{2}{x}$(x>0)上一动点,直线OA与双曲线y=$\frac{18}{x}$(x>0)交于点B,点C(9,0),连CB交双曲线y=$\frac{18}{x}$(x>0)于点D,连OD交双曲线y=$\frac{2}{x}$(x>0)于点E,若S△AOC=6S△ACE,则点A坐标为($\frac{9}{7}$,$\frac{14}{9}$).
如图,点A为双曲线y=$\frac{2}{x}$(x>0)上一动点,直线OA与双曲线y=$\frac{18}{x}$(x>0)交于点B,点C(9,0),连CB交双曲线y=$\frac{18}{x}$(x>0)于点D,连OD交双曲线y=$\frac{2}{x}$(x>0)于点E,若S△AOC=6S△ACE,则点A坐标为($\frac{9}{7}$,$\frac{14}{9}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com