
如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;
②4a﹣2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2.
上述4个判断中,正确的是( )
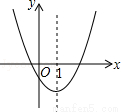
A. ①② B. ①④ C. ①③④ D. ②③④
B.
【解析】
试题分析:①∵抛物线与x轴有两个交点,∴b2﹣4ac>0,∴b2>4ac,故①正确;
②x=﹣2时,y=4a﹣2b+c,而题中条件不能判断此时y的正负,即4a﹣2b+c可能大于0,可能等于0,也可能小于0,故②错误;
③如果设ax2+bx+c=0的两根为α、β(α<β),那么根据图象可知不等式ax2+bx+c>0的解集是x<α或x>β,故③错误;
④∵二次函数y=ax2+bx+c的对称轴是直线x=1,∴x=﹣2与x=4时的函数值相等,
∵4<5,∴当抛物线开口向上时,在对称轴的右边,y随x的增大而增大,
∴y1<y2,故④正确.
故选B.
考点:1.二次函数图象与系数的关系2.二次函数图象上点的坐标特征3.二次函数与不等式(组).


科目:初中数学 来源:2014-2015学年内蒙古赤峰市宁城县七年级上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分10分)如图,已知线段AB=40厘米,E为AB的中点,C在EB上,F为CB的中点,且FB=6厘米,求CE的长.
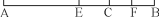
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省新泰市九年级上学期片区竞赛数学试卷(解析版) 题型:选择题
准备两张大小一样,分别画有不同图案的正方形纸片,把每张纸都对折、剪开,将四张纸片放在盒子里,然后混合,随意抽出两张正好能拼成原图的概率是( ).
A.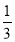 B.
B.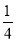 C.
C.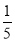 D.
D.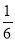
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期12月月考数学试卷(解析版) 题型:填空题
将二次函数y=2x2﹣1的图象沿y轴向上平移2个单位,所得图象对应的函数表达式为 _________ .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期12月月考数学试卷(解析版) 题型:选择题
在Rt△ABC中,∠C=90°,AC=12,BC=5,则sinA的值为( )
A、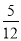 B、
B、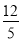 C、
C、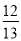 D、
D、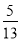
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期12月月考数学试卷(解析版) 题型:选择题
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
A.函数有最小值 B.对称轴是直线x=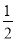
C.当x<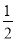 ,y随x的增大而减小D.当﹣1<x<2时,y>0
,y随x的增大而减小D.当﹣1<x<2时,y>0
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省射阳县九年级上学期期末考试数学试卷(解析版) 题型:解答题
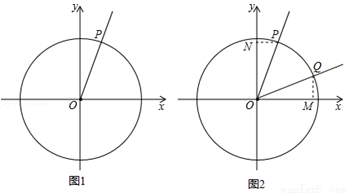
(本题满分12分)定义:如图1,射线OP与原点为圆心,半径为1的圆交于点P,记∠xOP=α,则点P的横坐标叫做角 的余弦值,记作
的余弦值,记作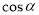 ;点P的纵坐标叫做角
;点P的纵坐标叫做角 的正弦值,记作
的正弦值,记作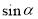 ;纵坐标与横坐标的比值叫做角
;纵坐标与横坐标的比值叫做角 的正切值,记作
的正切值,记作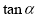 .
.
如:当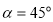 时, 点P的横坐标为
时, 点P的横坐标为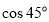 =
=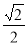 ,纵坐标为
,纵坐标为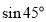 =
=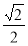 即P(
即P(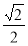 ,
,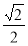 ).
).
又如:在图2中,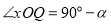 (
( 为锐角), PN
为锐角), PN
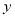 轴,QM
轴,QM
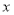 轴,易证△OQM≌△OPN, 则Q点的纵坐标
轴,易证△OQM≌△OPN, 则Q点的纵坐标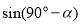 等于点P的横坐标
等于点P的横坐标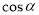 ,得
,得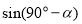 =
= 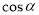 .
.
解决以下四个问题:
(1)当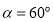 时,求点P的坐标;
时,求点P的坐标;
(2)当 是锐角时,则
是锐角时,则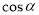 +
+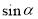 1(用>或<填空),
1(用>或<填空),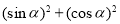 = ;
= ;
(3)求证: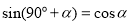 (
( 为锐角);
为锐角);
(4)求证:tan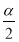 =
=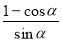 (
( 为锐角);
为锐角);
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省娄底市九年级上学期期末模拟考试数学试卷(解析版) 题型:解答题
(10分)如图,甲、乙两栋高楼的水平距离BD为90米,从甲楼顶部C点测得乙楼顶部A点的仰角α为30°,测得乙楼底部B点的俯角β为60°,求甲、乙两栋高楼各有多高?(计算过程和结果都不取近似值)
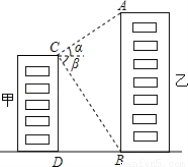
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com