
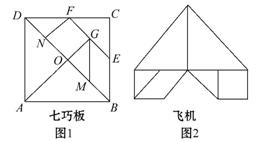
对正方形A BCD进行分割,如图1,其中E,F分别是BC,CD的中点,M,N,G分别是OB,OD,EF的中点,沿分化线可以剪出一副“七巧板”,用这些部件可以拼出很多图案,图2就是用其中6块拼出的“飞机”.若△GOM的面积为1,则“飞机”的面积为 .
BCD进行分割,如图1,其中E,F分别是BC,CD的中点,M,N,G分别是OB,OD,EF的中点,沿分化线可以剪出一副“七巧板”,用这些部件可以拼出很多图案,图2就是用其中6块拼出的“飞机”.若△GOM的面积为1,则“飞机”的面积为 .
14
【解析】连接AC,四边形ABCD是正方形,AC⊥BD,E,F分别是BC,CD的中点,EF∥BD,AC⊥EF,CF=CE,△EFC是等腰直角三角形,直线AC是△EFC底边上的高所在直线 ,根据等腰三角形“三线合一”,AC必过EF的中点G,点A,O,G和C在同一条直线上,OC=OB=OD,OC⊥OB,FG是△DCO的中位线,OG=CG=
,根据等腰三角形“三线合一”,AC必过EF的中点G,点A,O,G和C在同一条直线上,OC=OB=OD,OC⊥OB,FG是△DCO的中位线,OG=CG= OC,M,N分别是OB,OD的中点,OM=BM=
OC,M,N分别是OB,OD的中点,OM=BM= OB,ON=DN=
OB,ON=DN= OD,OG=OM=BM=ON=DN=
OD,OG=OM=BM=ON=DN= BD,等腰直角三角形GOM的面积为1,
BD,等腰直角三角形GOM的面积为1, OM·OG=
OM·OG= OM2=1,OM=
OM2=1,OM=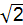 ,BD=4OM=4
,BD=4OM=4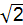 ,2AD2=BD2=32,AD=4,图2中飞机面积等于图1中多边形ABEFD的面积,飞机面积=正方形ABCD的面积-三
,2AD2=BD2=32,AD=4,图2中飞机面积等于图1中多边形ABEFD的面积,飞机面积=正方形ABCD的面积-三 角形CEF的面积=
角形CEF的面积= 16-2=14.
16-2=14.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
某公司有10名销售业务员,去年每人完成的销售额情况如表:
| 售额(万元) | 3 | 4 | 5 | 6 | 7 | 8 | 10 |
| 销售人数 | 1 | 3 | 2 | 1 | 1 | 1 | 1 |
问题:(1)求 10名销售员销售额的平均数、中位数和众数.(单位:万元)
10名销售员销售额的平均数、中位数和众数.(单位:万元)
(2 )为了调动员工积极性,公司准备采取超额有奖措施,请问把标准定为多少万元时最合适?
)为了调动员工积极性,公司准备采取超额有奖措施,请问把标准定为多少万元时最合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在周长为20cm的▱ABCD中,AB≠AD,AC,BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为( )
A.4 cm B.6 cm C.8 cm D.10 cm

查看答案和解析>>
科目:初中数学 来源: 题型:
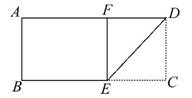
如图是一张矩形纸片ABCD,AD=10cm,若将纸片沿DE折叠,使DC落在DA上,点C的对应点为点F,若BE=6cm,则CD=( )
A.4cm B.6cm C.8cm D.10cm
查看答案和解析>>
科目:初中数学 来源: 题型:
美化城市,改善人们的居住环境已成为城市建设的一项重要内容,某市城区近几年来,通过拆迁旧房,植草,栽树,修建公园等措施,使城区绿化面积不断增加(如图所示)
(1)根据图中所提供的信息,回答下列问题:2001年的绿化面积为 公顷,比2000年增加了 公顷。在1999年,2000年,2001年这三年中,绿化面积增加最多的是 年。(3分)
(2)为满足城市发展的需要,计划到2003年使城区绿化地总面积达到72.6公顷,试求这两年(2001~2003)绿地面积的年平均增长率。(8分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com