【题目】列方程组解应用题：某学校在筹建数学实验室过程中，准备购进一批桌椅，现有三种桌椅可供选择：甲种每套150元，乙种每套210元，丙种每套250元。若该学校同时购买其中两种不同型号的桌椅50套，恰好花费了9000元，则共有哪几种购买方案？
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案科目：初中数学 来源： 题型：
【题目】某工厂生产A产品x吨所需费用为P元,而卖出x吨这种产品的售价为每吨Q元, 已知P=
x2+5x+1000,Q=-
+45.
(1)该厂生产并售出x吨,写出这种产品所获利润W(元)关于x(吨)的函数关系式;
(2)当生产多少吨这种产品,并全部售出时,获利最多?这时获利多少元? 这时每吨的价格又是多少元?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知一条抛物线经过A(0,3),B(4,6)两点,对称轴是x=
.
(1)求这条抛物线的关系式.
(2)证明:这条抛物线与x轴的两个交点中,必存在点C,使得对x轴上任意点D都有AC+BC≤AD+BD.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，如图，在△ABC中，∠B <∠C,AD,AE分别是△ABC的高和角平分线。
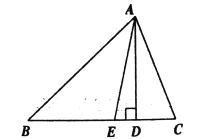
（1）若∠B=30°，∠C=50°，试确定∠DAE的度数；
（2）试写出∠DAE，∠B，∠C的数量关系，并证明你的结论。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=ax2-5x+c的图象如图所示,请根据图象回答下列问题:
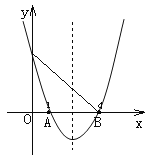
(1) a=_______,c=______.
(2)函数图象的对称轴是_________,顶点坐标P__________.
(3)该函数有最______值,当x=______时,y最值=________.
(4)当x_____时,y随x的增大而减小.当x_____时,y随x的增大而增大.
(5)抛物线与x轴交点坐标A_______,B________;与y轴交点C 的坐标为_______;
=_________,
=________.
(6)当y>0时,x的取值范围是_________;当y<0时,x的取值范围是_________.
(7)方程ax2-5x+c=0中△的符号为________.方程ax2-5x+c=0的两根分别为_____,____.
(8)当x=6时,y______0;当x=-2时,y______0.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在4×4的正方形网格中，每个小正方形的顶点称为格点，每个小正方形的边长均为1．在图①，图②中已画出线段AB，在图③中已画出点A．按下列要
求画图：
（1）在图①中，以格点为顶点，AB为一边画一个等腰三角形ABC；
（2）在图②中，以格点为顶点，AB为一边画一个正方形；
（3）在图③中，以点A为一个顶点，另外三个顶点也在格点上，画一个面积最大的正方
形，这个正方形的面积= ．
查看答案和解析>>
科目：初中数学 来源： 题型：
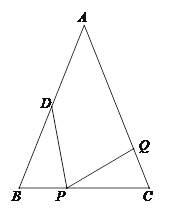
【题目】如图，已知△ABC中，AB=AC=6cm，BC=4cm，点D为AB的中点．
⑴如果点P在线段BC上以1cm/s的速度由点B向点C运动，同时，点Q在线段CA上由点C向点A运动．
①若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CPQ是否全等，请说明理由；
②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为______cm/s时，在某一时刻也能够使△BPD与△CPQ全等．
⑵若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都按逆时针方向沿△ABC的三边运动．求经过多少秒后，点P与点Q第一次相遇，并写出第一次相遇点在△ABC的哪条边上？
查看答案和解析>>
科目：初中数学 来源： 题型：
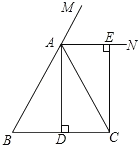
【题目】已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，
（1）求证：四边形ADCE为矩形；
（2）当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
