
【题目】已知梯形![]() 中,
中,![]() ∥
∥![]() ,且
,且![]() ,
,![]() ,
,![]() 。
。
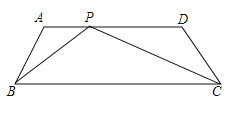
⑴如图,P为![]() 上的一点,满足∠BPC=∠A,求AP的长;
上的一点,满足∠BPC=∠A,求AP的长;
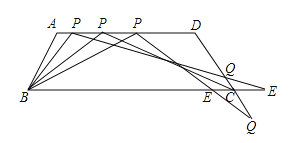
⑵如果点P在![]() 边上移动(点P与点
边上移动(点P与点![]() 不重合),且满足∠BPE=∠A,
不重合),且满足∠BPE=∠A,![]() 交直线
交直线![]() 于点E,同时交直线DC于点
于点E,同时交直线DC于点![]() 。
。
①当点![]() 在线段DC的延长线上时,设
在线段DC的延长线上时,设![]() ,CQ=y,求
,CQ=y,求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
②写CE=1时,写出AP的长(不必写解答过程)
【答案】⑴![]() 的长1或4;⑵①
的长1或4;⑵①![]()
![]() ;②
;②![]() 或3-
或3-![]()
【解析】
(1)当∠BPC=∠A时,∠A+∠APB+∠ABP=180°,而∠APB+∠BPC+∠DPC=180°,因此∠ABP=∠DPC,此时三角形APB与三角形DPC相似,那么可得出关于AP,PD,AB,CD的比例关系式,AB,CD的值题中已经告诉,可以先用AP表示出PD,然后代入上面得出的比例关系式中求出AP的长.
(2)①与(1)的方法类似,只不过把DC换成了DQ,那么只要用DC+CQ就能表示出DQ了.然后按得出的关于AB,AP,PD,DQ的比例关系式,得出x,y的函数关系式.
②和①的方法类似,但是要多一步,要先通过平行得出三角形PDQ和CEQ相似,根据CE的长,用AP表示出PD,然后根据PD,DQ,QC,CE的比例关系用AP表示出DQ,然后按①的步骤进行求解即可.
解:⑴![]() ,
,![]() ,
,
![]() ,
,
又![]() 梯形
梯形![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,
,![]() ,
,
![]() ,
,
解得![]() ,
,![]() ,
,
![]() 的长1或4;
的长1或4;
⑵①由⑴易得![]() (如图),
(如图),
![]() ,即
,即![]() ,
,
![]()
![]()
②当CE=1时,
∵△PDQ∽△ECQ,
∴![]() ,
,
![]() 或
或![]() ,
,
![]() ,
,
解得:AP=2或3![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于点P(x,y)和Q(x,y′),给出如下定义:如果y′=![]() ,那么称点Q为点P的“伴随点”.
,那么称点Q为点P的“伴随点”.
例如:点(5,6)的“伴随点”为点(5,6);点(﹣5,6)的“伴随点”为点(﹣5,﹣6).
(1)直接写出点A(2,1)的“伴随点”A′的坐标.
(2)点B(m,m+1)在函数y=kx+3的图象上,若其“伴随点”B′的纵坐标为2,求函数y=kx+3的解析式.
(3)点C、D在函数y=﹣x2+4的图象上,且点C、D关于y轴对称,点D的“伴随点”为D′.若点C在第一象限,且CD=DD′,求此时“伴随点”D′的横坐标.
(4)点E在函数y=﹣x2+n(﹣1≤x≤2)的图象上,若其“伴随点”E′的纵坐标y′的最大值为m(1≤m≤3),直接写出实数n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】使得函数值为0的自变量的值称为函数的零点.例如,对于函数y=x﹣1,令y=0可得x=1,我们说1是函数y=x﹣1的零点.已知函数y=x2﹣2mx﹣2(m+3)(m为常数)
(1)当m=0时,求该函数的零点.
(2)证明:无论m取何值,该函数总有两个零点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1=k1x+b与反比例函数![]() 的图象交于A,B两点(点A在点B左侧),已知点A的坐标是(6,2)点B的纵坐标是﹣3.
的图象交于A,B两点(点A在点B左侧),已知点A的坐标是(6,2)点B的纵坐标是﹣3.
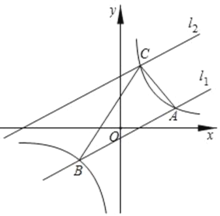
(1)求反比例函数和直线l1的表达式;
(2)根据图象直接写出k1x+b>![]() 的解集;
的解集;
(3)将直线l1:![]() 沿y轴向上平移后的直线l2与反比例函数
沿y轴向上平移后的直线l2与反比例函数![]() 在第一象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第一象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备从体育用品商店一次性购买若干个篮球和足球(每个篮球的价格相同,每个足球的价格相同),购买1个足球和2个篮球共需270元;购买2个足球和3个篮球共需464元.
(1)问足球和篮球的单价各是多少元?
(2)若购买足球和篮球共20个,且购买篮球的个数不超过足球个数的2倍,购买球的总费用不超过1910元,问该学校有哪几种不同的购买方案?哪种方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
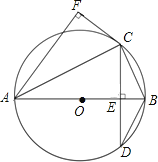
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,CF⊥AF,且CF=CE.
(1)求证:CF是⊙O的切线;
(2)若sin∠BAC=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
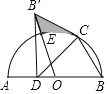
【题目】如图,以AB为直径,点O为圆心的半圆上有一点C,且∠ABC=60°,点D为AO上一点.将△DBC沿直线DC对折得到△DB'C,点B的对应点为B′,且B'C与半圆相切于点C,连接B′O交半圆于点E.
(1)求证:B'D⊥AB;
(2)当AB=2时,求图中阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为培养学生的创造性思维,学校举行科技小制作比赛.对公开征集到的科技小制作作品的数量进行了分析统计,并制作了如下统计图.
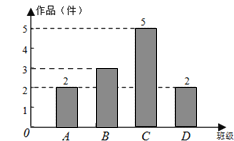
(1)学校共征集到作品共 件;
(2)经过评选后,有2名男生和2名女生获得一等奖.现要从这4位同学中抽两人去参加表彰座谈会,请用树状图或列表法求出恰好抽中一男一女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com