
 如图,某房地产公司要在一块地皮(矩形OBCD)上建造一个公园(矩形GHCK),为了使文物保护区△OEF不被破坏,公园的顶点G不能在文物保护区内.已知OB=200m.OD=160m,OE=60m,OF=40m.当GH多长时,公园的面积最大?最大面积是多少(精确到1m2)?
如图,某房地产公司要在一块地皮(矩形OBCD)上建造一个公园(矩形GHCK),为了使文物保护区△OEF不被破坏,公园的顶点G不能在文物保护区内.已知OB=200m.OD=160m,OE=60m,OF=40m.当GH多长时,公园的面积最大?最大面积是多少(精确到1m2)? 分析 作辅助线,构建相似三角形,先设MG=xm,公园面积为ym2,根据平行线分线段成比例定理列比例式,表示出DM的长,利用矩形面积公式=长×宽列等式,得出二次函数关系式,求最值即可.
解答 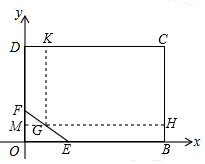 解:延长HG交OD于M,
解:延长HG交OD于M,
设MG=xm,公园面积为ym2,则GH=(200-x)m,
∵GH∥OB,
∴MG∥OB,
∴$\frac{MG}{OE}=\frac{FM}{OF}$,
∴$\frac{x}{60}=\frac{FM}{40}$,
∴FM=$\frac{2}{3}$x,
∴OM=40-$\frac{2}{3}$x,
∴DM=OD-OM=160-(40-$\frac{2}{3}$x)=$\frac{2}{3}$x+120,
∴y=GH•DM=(200-x)($\frac{2}{3}$x+120)=-$\frac{2}{3}{x}^{2}$+$\frac{40}{3}$x+24000,
因为-$\frac{2}{3}$<0,所以当x=-$\frac{\frac{40}{3}}{2×(-\frac{2}{3})}$=10时,y有最大值,即GH=200-10=190,
y最大值=(200-10)($\frac{2}{3}$×10+120)=$\frac{72200}{3}$≈24067,
答:当GH为190m时,公园的面积最大,最大面积是24067m2.
点评 本题是二次函数的应用,属于图形面积问题;恰当地设出自变量与函数,找出等量关系式是做好本题的关键;将最大面积问题转化为二次函数的最值问题,同时要注意实际问题中的取值范围.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | +2 | B. | -3 | C. | -1 | D. | +4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 信件质量/克 | 0<m≤20 | 20<m≤40 | 40<m≤60 |
| 邮费/元 | 0.80 | 1.20 | 1.60 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
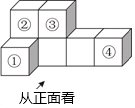 如图,是由7个大小相同的小正方体堆砌而成的几何体,若从标有①、②、③、④的四个小正方体中取走一个后,余下几何体与原几何体的主视图相同,则取走的正方体是( )
如图,是由7个大小相同的小正方体堆砌而成的几何体,若从标有①、②、③、④的四个小正方体中取走一个后,余下几何体与原几何体的主视图相同,则取走的正方体是( )| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 有理数a,b,c在数轴上的位置如图,化简|a|-|a+b|+|c-a|+|b-c|的结果为( )
有理数a,b,c在数轴上的位置如图,化简|a|-|a+b|+|c-a|+|b-c|的结果为( )| A. | -a | B. | 2a-2b | C. | 2c-a | D. | a |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 50(100-x)千克 | B. | (50×100-x)千克 | C. | 100(50-x)千克 | D. | 50x千克 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
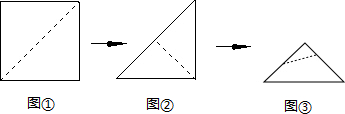
| A. | 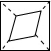 | B. | 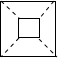 | C. | 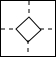 | D. | 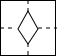 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com