
【题目】在直角坐标系xOy中,已知点P是反比例函数y=![]() (x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(1)如图1,当⊙P运动到与x轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由;
(2)如图2,当⊙P运动到与x轴相交,设交点为点B、C.当四边形ABCP是菱形时,求出点A、B、C的坐标;
(3)在(2)的条件下,求出经过A、B、C三点的抛物线的解析式.

【答案】(1)四边形OKPA是正方形,理由见解析;(2)A(0,![]() ),B(1,0),C(3,0);(3)y=
),B(1,0),C(3,0);(3)y=![]() x2﹣
x2﹣![]() x+
x+![]() .
.
【解析】
(1)先证明四边形OKPA是矩形,又PA=PK,故可得四边形OKPA是正方形;
(2)证明△PBC为等边三角形;在Rt△PBG中,∠PBG=60°,设PB=PA=a,BG=![]() ,由勾股定理得:PG=
,由勾股定理得:PG=![]() ,所以P(a,
,所以P(a,![]() ),将P点坐标代入y=
),将P点坐标代入y=![]() ,求出PG=
,求出PG=![]() ,PA=BC=2,又四边形OGPA是矩形,PA=OG=2,BG=CG=1,故OB=OG﹣BG=1,OC=OG+GC=3,即可求解;
,PA=BC=2,又四边形OGPA是矩形,PA=OG=2,BG=CG=1,故OB=OG﹣BG=1,OC=OG+GC=3,即可求解;
(3)设二次函数的解析式为:y=ax2+bx+c,将(2)中三点坐标分别代入,利用待定系数法进行求解即可.
(1)四边形OKPA是正方形,
理由:∵⊙P分别与两坐标轴相切,
∴PA⊥OA,PK⊥OK,
∴∠PAO=∠OKP=90°,
又∵∠AOK=90°,
∴∠PAO=∠OKP=∠AOK=90°,
∴四边形OKPA是矩形,
又∵PA=PK,
∴四边形OKPA是正方形;
(2)连接PB,过点P作PG⊥BC于G,
∵四边形ABCP为菱形,∴BC=PA=PB=PC,
∴△PBC为等边三角形,
在Rt△PBG中,∠PBG=60°,
设PB=PA=a,BG=![]() ,
,
由勾股定理得:PG=![]() ,
,
所以P(a,![]() ),将P点坐标代入y=
),将P点坐标代入y=![]() ,
,
解得:a=2或﹣2(舍去负值),
∴PG=![]() ,PA=BC=2,
,PA=BC=2,
又四边形OGPA是矩形,PA=OG=2,BG=CG=1,
∴OB=OG﹣BG=1,OC=OG+GC=3.
∴A(0,![]() ),B(1,0),C(3,0);
),B(1,0),C(3,0);
(3)二次函数的解析式为:y=ax2+bx+c,
根据题意得: ,
,
解得: ,
,
∴二次函数的解析式为:y=![]() x2﹣
x2﹣![]() x+
x+![]() .
.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,某汽车在路面上朝正东方向匀速行驶,在A处观测到楼H在北偏东60°方向上,行驶1小时后到达B处,此时观测到楼H在北偏东30°北方向上,那么汽车由B处到达离楼H距离最近的位置C时,需要继续行驶的时间为( )
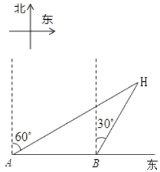
A. 60分钟B. 30分钟C. 15分钟D. 45分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
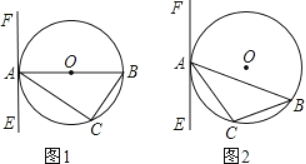
【题目】已知△ABC内接于⊙O,过点A作直线EF,
(1)如图1,若AB为直径,要使得EF是⊙O的切线,还需要添加的条件是(只须写出两种不同情况)① 或② .
(2)如图2,若AB为非直径的弦,∠CAE=∠B,试说明EF是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
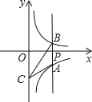
【题目】如图,过x轴正半轴上的任意一点P,作y轴的平行线,分别与反比例函数y=﹣![]() 和y=
和y=![]() 的图象交于A、B两点.若点C是y轴上任意一点,连接AC、BC,则△ABC的面积为( )
的图象交于A、B两点.若点C是y轴上任意一点,连接AC、BC,则△ABC的面积为( )
A. 3B. 4C. 5D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+mx﹣6=0.
(1)求证:不论m为何实数,方程总有两个不相等的实数根;
(2)若m=1,用配方法解这个一元二次方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
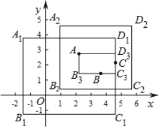
【题目】在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:
如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1,A2B2C2D2,AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.
(1)已知A(﹣2,3),B(5,0),C(t,﹣2).
①当t=2时,点A,B,C的最优覆盖矩形的面积为 ;
②若点A,B,C的最优覆盖矩形的面积为40,求直线AC的表达式;
(2)已知点D(1,1).E(m,n)是函数y=![]() (x>0)的图象上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
(x>0)的图象上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,关于x的方程a(1﹣x2)+2bx+c(1+x2)=0有两个相等实根,且3c=a+3b
(1)试判断△ABC的形状;
(2)求sinA+sinB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com