
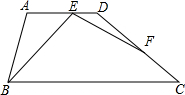
 (2012•大连)如图,梯形ABCD中,AD∥BC,∠ABC=2∠BCD=2α,点E在AD上,点F在DC上,且∠BEF=∠A.
(2012•大连)如图,梯形ABCD中,AD∥BC,∠ABC=2∠BCD=2α,点E在AD上,点F在DC上,且∠BEF=∠A.| EB | EF |
| OE |
| OD |
| OB |
| OF |
| EB |
| EF |
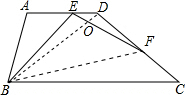 (2)EB=EF.
(2)EB=EF.| 1 |
| 2 |
| OE |
| OD |
| OB |
| OF |
| OE |
| OB |
| OD |
| OF |
 (3)解:延长AB至G,使AG=AE,连接GE,
(3)解:延长AB至G,使AG=AE,连接GE,| 180°-∠A |
| 2 |
| 180°-(180°-2α) |
| 2 |
| EB |
| EF |
| BG |
| DE |
| EB |
| EF |
| BG |
| DE |
| (n+1-m)DE |
| DE |


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
| 投篮次数(n) | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
| 投中次数(m) | 28 | 60 | 78 | 104 | 123 | 152 | 251 |
| 投中频率(m/n) | 0.56 | 0.60 | 0.52 | 0.52 | 0.49 | 0.51 | 0.50 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•大连)如图,为了测量电线杆AB的高度,小明将测量仪放在与电线杆的水平距离为9m的D处.若测角仪CD的高度为1.5m,在C处测得电线杆顶端A的仰角为36°,则电线杆AB的高度约为
(2012•大连)如图,为了测量电线杆AB的高度,小明将测量仪放在与电线杆的水平距离为9m的D处.若测角仪CD的高度为1.5m,在C处测得电线杆顶端A的仰角为36°,则电线杆AB的高度约为查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•大连)如图,矩形ABCD中,AB=15cm,点E在AD上,且AE=9cm,连接EC,将矩形ABCD沿直线BE翻折,点A恰好落在EC上的点A′处,则A′C=
(2012•大连)如图,矩形ABCD中,AB=15cm,点E在AD上,且AE=9cm,连接EC,将矩形ABCD沿直线BE翻折,点A恰好落在EC上的点A′处,则A′C=查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•大连)如图,抛物线y=ax2+bx+c经过A(-
(2012•大连)如图,抛物线y=ax2+bx+c经过A(-| 3 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com