
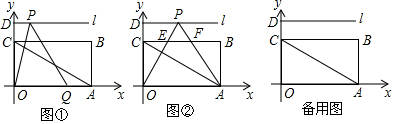
���� ��1�����ı���OABC�Ǿ��Σ����ݾ��ε����ʣ�������õ�B�����ꣻ�����к�����������á�CAO�Ķ�����
��2�������POA�������֤����PEF�ס�POA���ɶ�Ӧ�ߵıȵ������Ʊȵó����Ʊȣ��������ȣ����ɵó��ı��ε������
��3���ֱ��MN=AN��AM=AN��AM=MNȥ������⼴����ô𰸣�
��� �⣺��1�����ı���OABC�Ǿ��Σ�
��AB=OC��OA=BC��OA��BC��
��A��6��0����C��0��2$\sqrt{3}$����
���B����������6��2$\sqrt{3}$����
�ʴ�Ϊ����6��2$\sqrt{3}$����30�㣻
�ڡ�tan��CAO=$\frac{OC}{OA}$=$\frac{2\sqrt{3}}{6}$=$\frac{\sqrt{3}}{3}$��
���CAO=30��
�ʴ�Ϊ����6��2$\sqrt{3}$����30��
��2����POA�����=$\frac{1}{2}$��6��3$\sqrt{3}$=9$\sqrt{3}$��
��OA��BC��
���PEF�ס�POA�����Ʊ�Ϊ$\frac{DC}{DO}$=$\frac{3\sqrt{3}-2\sqrt{3}}{3\sqrt{3}}$=$\frac{1}{3}$��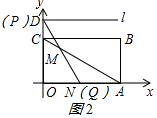
��$\frac{{S}_{��PWF}}{{S}_{��POA}}$=$\frac{1}{9}$��
���ı���OEFQ�����=$\frac{8}{9}$S��POA=$\frac{8}{9}$��9$\sqrt{3}$=8$\sqrt{3}$��
��3����DP�ij�Ϊm����������ۣ�
����ͼ2��MN=AN=3ʱ��
���AMN=��MAN=30�㣬
���MNO=60�㣬
�ߡ�PQO=60�㣬
����MQO=60��
���N��Q�غϣ�
���P��D�غϣ�
���ʱDP=0��
����ͼ3��AM=ANʱ����MJ��x����J��PI��x����I��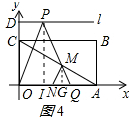
MJ=MQ•sin60��=AQ•sin60��=��OA-IQ-OI��•sin60��=$\frac{\sqrt{3}}{2}$��3-m��=$\frac{1}{2}$AM=$\frac{1}{2}$AN=$\frac{3}{2}$��
�ɵ�$\frac{\sqrt{3}}{2}$��3-m��
��ã�m=3-$\sqrt{3}$��
��AM=NMʱ����ʱM�ĺ�������4.5��
��ͼ4������P��PI��OA��I������M��MG��OA��G��
��MG=$\frac{\sqrt{3}}{2}$��
��QI=$\frac{PI}{tan60��}$=$\frac{3\sqrt{3}}{\sqrt{3}}$=3��GQ=$\frac{MG}{tan60��}$=$\frac{1}{2}$��
��IG=3-0.5=2.5��AG=$\frac{1}{2}$AN=1.5��
��OI=2��
��m=2��
�������������ڵ�P��ʹ��MNAΪ���������Σ��߶�DP�ij�Ϊ0��3-$\sqrt{3}$��2��
���� �������ı����ۺ���Ŀ�������˾��ε����ʣ����������ε��ж������ʡ����������ε������Լ�ֱ�������ε����ʵ�֪ʶ�������ۺ��Խ�ǿ���ѶȽϴ�ע�����ν��˼�����������˼���Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��a=0����ab=0 | |
| B�� | �ڴ�����ȣ���ֱ��ƽ�� | |
| C�� | ����������ȣ���ô�������Ƕ�Ϊ30�� | |
| D�� | ��|a|=|b|����a=b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x+2��2=5 | B�� | ��x-2��2=3 | C�� | ��x-2��2=5 | D�� | ��x+2��2=3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��С���ڲٳ��ϻ���һ���뾶�ֱ�Ϊ1��2��3��ͬ��Բ��ͼ�������������ͼ���������һ��ʯ�ӣ����ʯ��ǡ����������C�еĸ����ǣ�������
��ͼ��С���ڲٳ��ϻ���һ���뾶�ֱ�Ϊ1��2��3��ͬ��Բ��ͼ�������������ͼ���������һ��ʯ�ӣ����ʯ��ǡ����������C�еĸ����ǣ�������| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{5}$ | C�� | $\frac{1}{7}$ | D�� | $\frac{1}{9}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
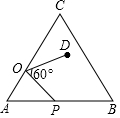 ��ͼ���ڵȱߡ�ABC�У�AC=9����O��AC�ϣ���AO=3����P��AB��һ���㣬����OP�����߶�OP�Ƶ�O��ʱ����ת60��õ��߶�OD��Ҫʹ��Dǡ������BC�ϣ���AP�ij��ǣ�������
��ͼ���ڵȱߡ�ABC�У�AC=9����O��AC�ϣ���AO=3����P��AB��һ���㣬����OP�����߶�OP�Ƶ�O��ʱ����ת60��õ��߶�OD��Ҫʹ��Dǡ������BC�ϣ���AP�ij��ǣ�������| A�� | 3 | B�� | 5 | C�� | 6 | D�� | 8 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com